Fuzzy Predator-Prey Systems by Extended Runge-Kutta Method with Polynomial Interpolation Technique

Abstract

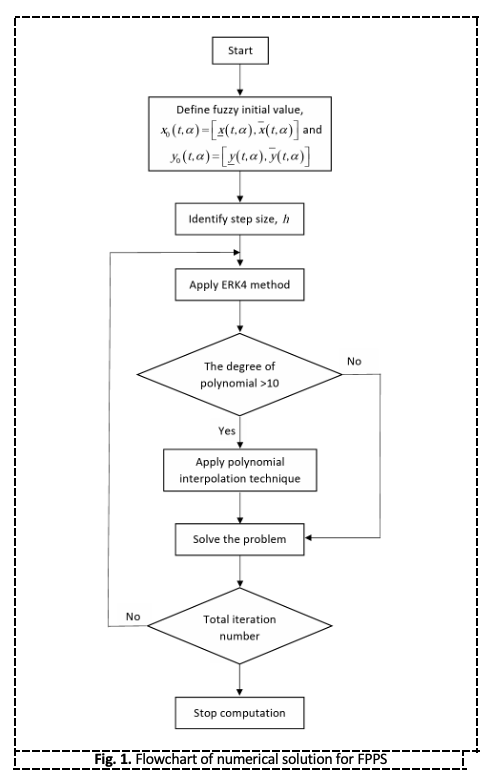
The growing significance of uncertainty quantification in mathematical modeling of physical phenomena is evident, with fuzzy sets emerging as an alternative approach. This paper focuses on exploring a numerical method for addressing fuzzy differential equations in two-dimensional problems like fuzzy predator-prey systems. The numerical solution employed the extended Runge-Kutta fourth-order method. To overcome challenges related to polynomial fuzzy differential equations, a combination of the polynomial interpolation technique and the extended Runge-Kutta fourth-order method was applied, mitigating the issues associated with high-degree polynomials. The proposed approach for fuzzy predator-prey systems is briefly described, accompanied by a numerical example. The obtained results underscore the efficacy of the extended Runge-Kutta fourth-order method with polynomial interpolation, showcasing its remarkable accuracy and potential as an alternative method for addressing various uncertainty-related problems.