Bi-stability Study of Double Diffusive Convection Using the Carreau- Yasuda Model in a Shallow Horizontal Porous Layer Filled with a Non- Newtonian Fluid

Abstract

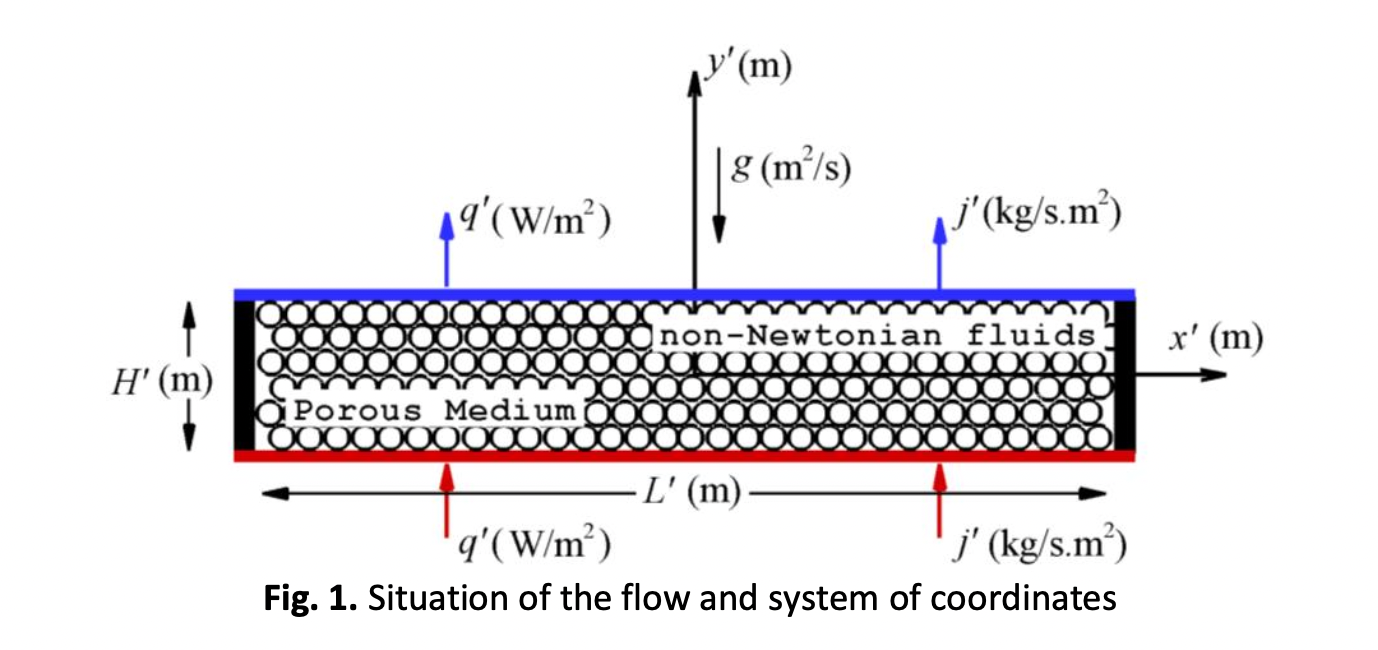
The onset of non-linear convection in a horizontal porous layer saturated by a shear- thinning liquid is studied. The Carreau-Yasuda model is utilized for modeling the behavior of the working medium. Constant fluxes of heat and mass are imposed on the horizontal walls of the cavity, while the vertical sides are assumed adiabatic and impermeable. The parallel flow approximation and the finite difference approach are used to conduct the investigation analytically and numerically, respectively. By considering an infinitesimal perturbation, the linear stability analysis of the diffusive and convective states is conducted based on the finite element method. The theory of linear stability is employed to determine the critical Rayleigh number for the onset of motion from the rest state as well as the onset of Hopf bifurcation, transition from the stationary to oscillatory convection. Overall, the Carreau-Yasuda rheological parameters have a significant impact on the thresholds of convection. The most interesting findings of this study is highlighting the existence of a bi-stability phenomenon, i.e., the existence of two steady-state solutions, which was not observed before in non-Newtonian fluids convection.