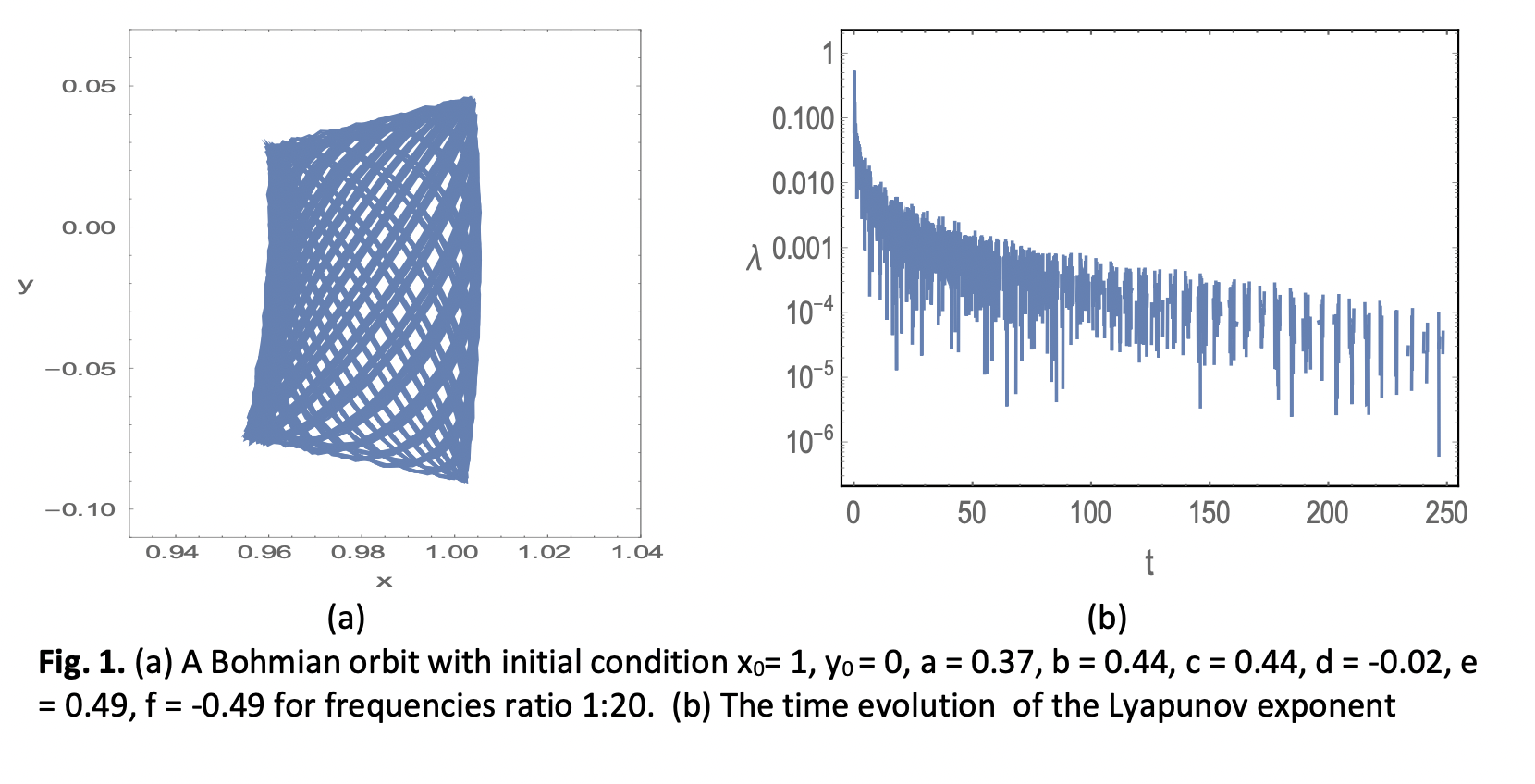
Chaos In 2D Bohmian Trajectories of Commensurate Harmonics Oscillators

Abstract

Particle trajectories guided by the wave function are well-defined through Bohmian mechanics, which is a causal interpretation of quantum mechanics. Periodic and chaotic behaviours could be exhibited from the certain classical integrable systems that have been shown within this framework. In this study, we developed Mathematica programs to plot the Bohmian trajectories and Lyapunov exponents. These programs serve as computer experiments for numerical generation and illustration of the results. We show that the behaviours of commensurate two-dimensional harmonic oscillator systems are dependent on ratios of frequency.