Optimized bi-Quadratic Trigonometric Bézier Curve using Particle Swarm Optimization

Abstract

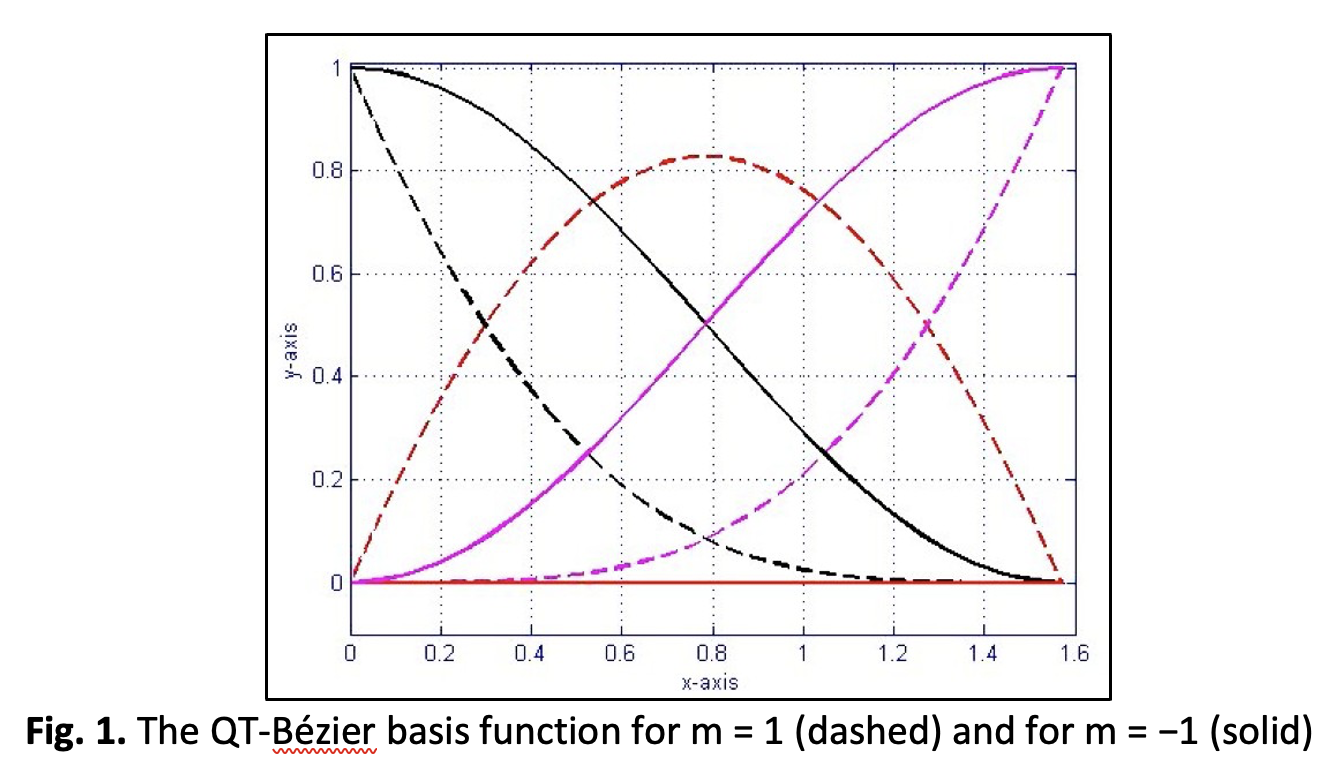
This paper introduces a new approach, namely an optimized bi-QT-Bézier, for fitting curves to given 2D polygons and their two end tangents. The conventional approach includes additional constraints to uniquely determine the biarc. The main idea is to exploit the inherent freedom in the choice of the  to achieve an optimized curve that is closer to its control polygon. The proposed method integrates the formulation of a single biarc with the Quadratic Trigonometric (QT)-Bézier curve and Particle Swarm Optimization (PSO). The proposed bi-QT-Bézier is advantageous in curve fitting as it provides an optimized value of  from the PSO method. Besides, the proposed scheme also provides the flexibility to construct the desired curve. The proposed approach generates a curve with a smaller distance between the curve and its control polygon compared to the previous optimal single biarc and Sabin’s constraint. An experimental result is provided to demonstrate the usefulness and efficiency of the proposed method. The implementation of the optimized bi-QT-Bézier to fit a circle and complex shape will also be analyzed. This proves that the proposed method is an excellent tool in curve fitting.