The Topological Indices of the p-Subgroup Graph of Dihedral Groups

Abstract

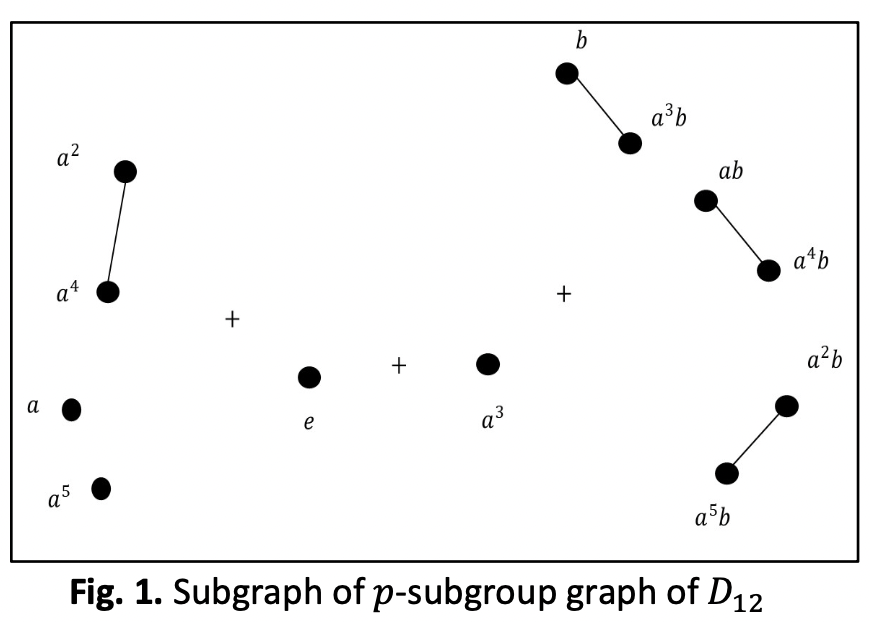
A topological index is a number generated from a molecular structure that signifies the molecule’s fundamental structural characteristics. This correlation between the index and various physical attributes is based on an algebraic quantity related to the chemical structure. Many topological indices, such as the Wiener index, first and second Zagreb indices, can be employed to determine various properties, including chemical activity, thermodynamic properties, physicochemical activity, and biological activity. Meanwhile, the p-subgroup graph of a group G is defined as a graph whose vertices represent the elements of the group, and two vertices are adjacent if and only if the order of the subgroup is a prime power. The main objective of this paper is to establish the general formula for certain topological indices, specifically the Wiener index, first Zagreb index, and second Zagreb index for the -subgroup graph associated with dihedral groups.