Solution of Volterra Integral Equations of the Second Kind with Weakly Singular Kernels Using Legendre Polynomials
DOI:
https://doi.org/10.37934/araset.53.1.3243Keywords:
Volterra integral equations, Weakly singular kernels, Legendre polynomials, Approximation, Computational methodAbstract
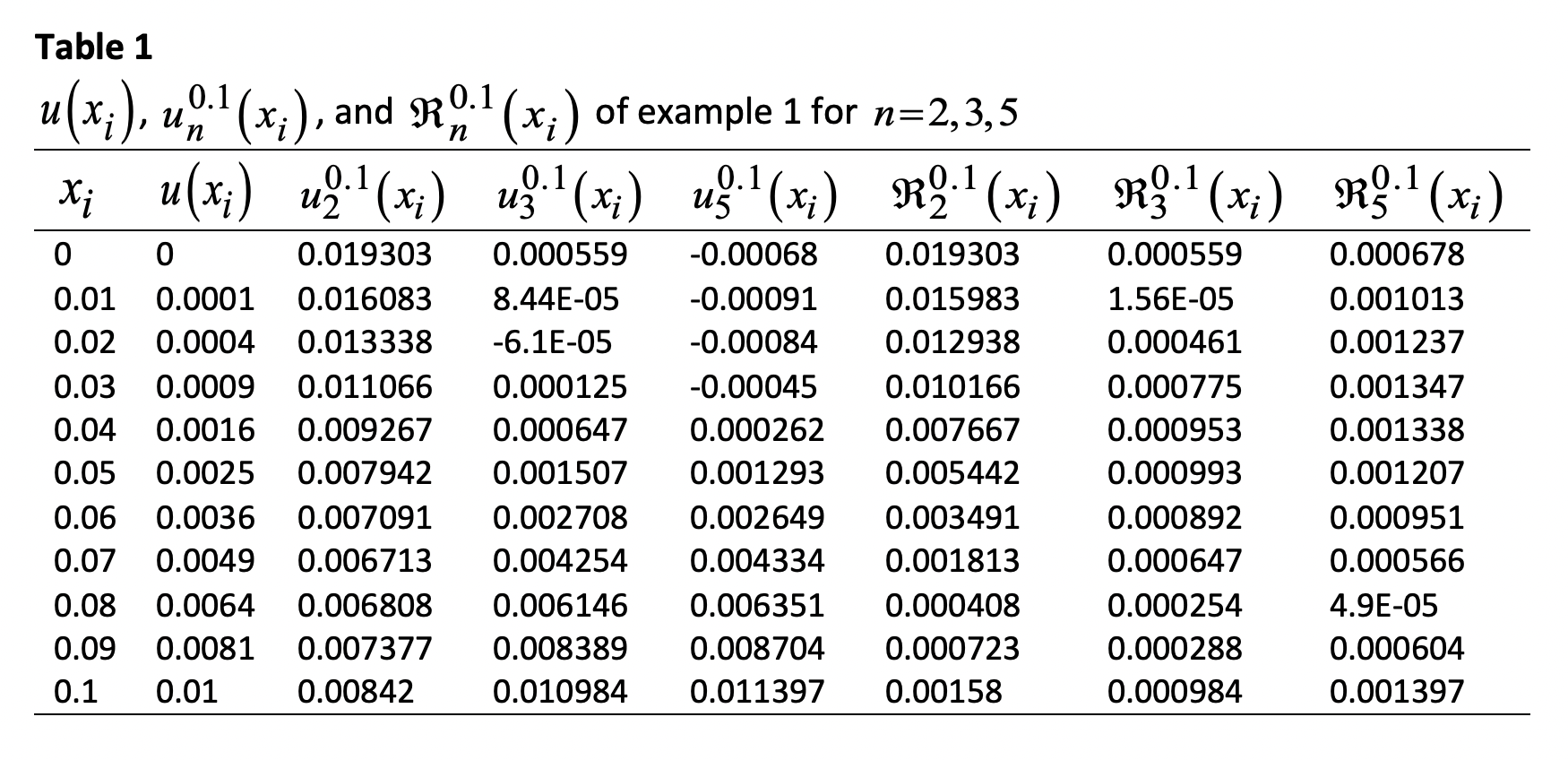
The shifted Legendre polynomials of the first kind are employed to solve second kind Volterra integral equations with weakly singular kernels. In this method the unknown function and the data function are approximated through three matrices, while the kernel function is approximated through five matrices. Regarding the kernel's two variables, it will be approximated twice, first with respect to variable x and second with respect to variable t. The singularity of the kernel is removed analytically. It is proved that the solution is equivalent to an algebraic linear system without applying the collocation method. Two numerical experiments are solved to illustrate the efficiency of the proposed method.
Downloads