Effect of Magnetic Field on the Developing Thermal Field in a Duct Filled with Porous Media under Local Thermal Non-Equilibrium with a Nonlinear Flow Model
DOI:
https://doi.org/10.37934/arfmts.103.1.87104Keywords:
Local thermal non-equilibrium model, Darcy Brinkman Forchheimer model, Hartmann number, porous medium, wall heat fluxAbstract
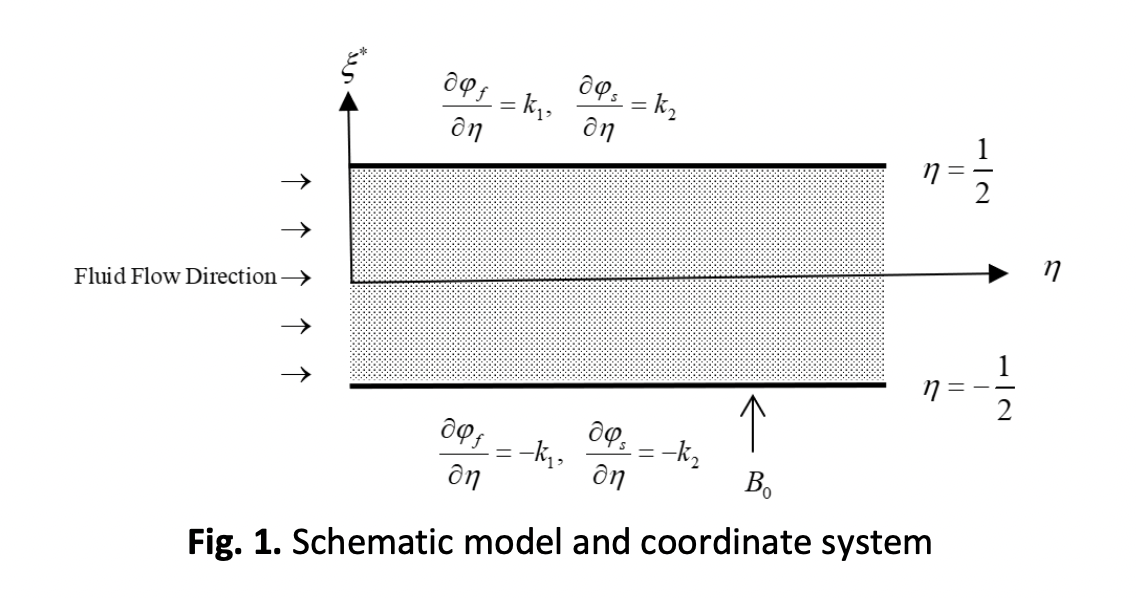
In this article, the numerical study of the influence of a magnetic field at the laminar forced convection in a thermally developing region coming under the influence of local thermal non-equilibrium (LTNE) of parallel plate channels completely immersed in the porous material is investigated. Constant wall heat flux boundary conditions are applied to the walls of the channel. In the nonlinear flow model, the Darcy-Brinkman-Forchheimer equation governs the flow field in the porous region, which is assumed to be unidirectional. The system is defined by certain well-known parameters, these being Darcy number (Da), thermal conductivity ratio (κ), Forchheimer number (F), Hartmann number (M), and Biot number (Bi). Numerical solutions have been obtained by applying a successive accelerated replacement (SAR) scheme. Exact solutions for the dimensionless temperature and the fully developed Nusselt number in the absence of the Forchheimer number (F = 0), for the fully developed thermal field, are obtained for the linear flow model, the Darcy-Brinkman model. Plots are given for the dimensionless temperature profiles in the fluid and solid phases, wall temperature, as well as the local Nusselt number at the parallel plate channel, which has been displayed. The effect of the magnetic field and the thermal conductivity ratio has a significant effect on the local Nusselt number.
Downloads