Partial Slip Effects on MHD Peristaltic Flow of Carreau-Yasuda Fluid (CY) Through a Planner Micro-Channel
DOI:
https://doi.org/10.37934/arfmts.104.2.6585Keywords:
Carreau-Yasuda fluid model, velocity slip parameter, convective heat and mass parametersAbstract
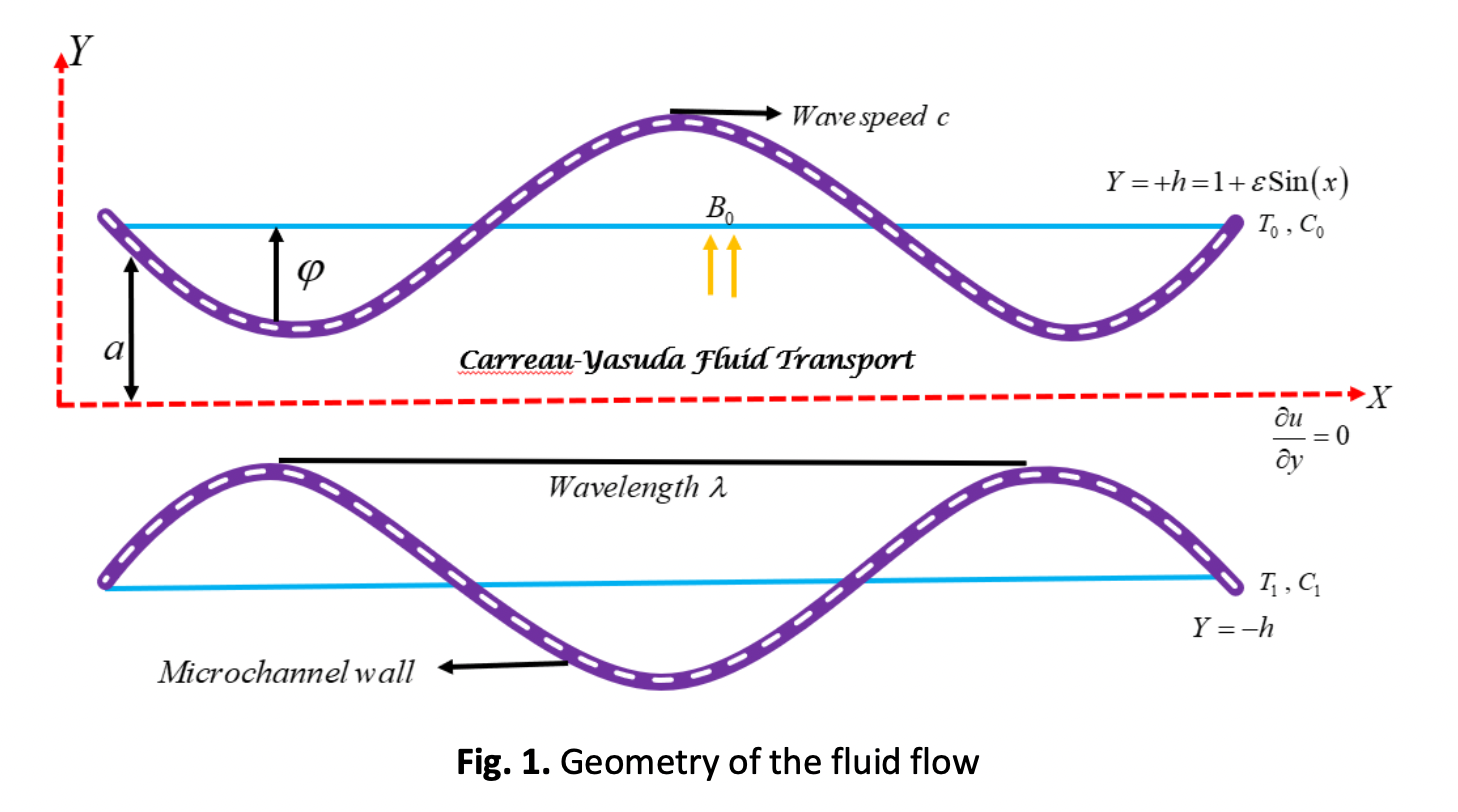
In modern applied mathematics, engineering, and the physiological world, the concept of peristalsis is of great significance. The present article concentrates on the peristaltic movement of Carreau-Yasuda fluid through planner micro-channel under the influence of applied magnetic field and partial slip conditions. The governing system of equations are nondimensionalized and transformed using basic assumptions such as long wavelength and low Reynolds number. A bulti-in route "ND solve" in Mathematica exercised to solve obtained nonlinear coupled equations with appropriate boundary conditions. Obtained results are elucidated by plotting graphs for different physiological constraints such as velocity, temperature, and concentration. Physical characteristics such as skin friction, Nusselt number and Sherwood number are discussed via table results. The typical character of this work e.g. flow index parameter exhibits that the apparent fluid viscosity becomes high when it has a higher value due to which fluid faces more resistance and the presence of a higher magnetic effect predicts the decreasing behavior on velocity. Additionally, the trapping phenomenon explains bolus movement and are discussed briefly.
Downloads