Stability Analysis of The Stagnation-Point Flow and Heat Transfer Over a Shrinking Sheet in Nanofluid in The Presence of MHD and Thermal Radiation

Abstract

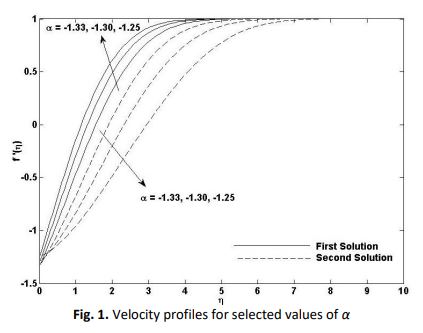
Recent developments in the field of fluid dynamics have led to a new interest in stability analysis. The numerical solution obtained from the problems of the flow at the stagnation point, as well as the heat transfer with MHD and thermal radiation effects over a shrinking sheet, is used to carry out a stability analysis. The flow of this problem is considered in nanofluids and Buongiorno's model is employed. The boundary layer equation is obtained by reducing the governing equations to an ordinary differential equation. Partial differential equations are converted to ordinary differential equations using a suitable similarity transformation. The bvp4c simulation on Matlab is then used to solve ordinary differential equations. According to the numerical data, the dual solutions occur in a specific range of α. The parameter α refers to the stretching/shrinking where shrinking (less than 0) is the main reason the dual solution exists. The stability analysis is presented graphically and in tabular form to prove that there are two solutions to the problem and only one of them is stable. As a result, our research shows that the solution is only stable in the first solution, but not in the second.