Rayleigh-Benard Convection Inside Square Cavities Filled with Thermodependent Non-Newtonian Fluids and Subjected to External Magnetic Field
DOI:
https://doi.org/10.37934/arfmts.110.2.138156Keywords:
Natural convection, Rayleigh-Benard, non-Newtonian fluid, magnetic field, power law, temperature dependence on viscosityAbstract
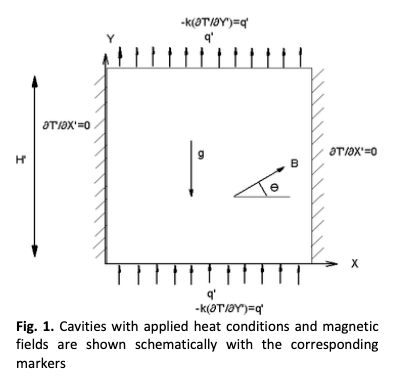
The aim of this study is to numerically evaluate the Rayleigh-Benard natural convection magnetohydrodynamic (MHD) of a non-Newtonian fluid along a square cavity whose viscosity depends on the temperature. The rheological behavior of the fluids under consideration is represented using the Ostwald-De-Weale power law. Subsequently, the dominant equations are transformed into a non-dimensional form and computed using the finite volume method (FVM). The literature was used to validate the model, and excellent agreement was achieved by varying the fluid characteristics with Prandtl numbers , Hartmann numbers, , Rayleigh numbers, , the behavior index, n, and inclination angle, . The numerical results are discussed in terms of velocity, mean Nusselt number , maximum current function , streamlines, and isotherms. The study finds that the onset of convection is delayed with increasing values of n and Ha. Additionally, it revealed that the flow intensity and heat transfer decrease as the Hartmann number rises for both Newtonian and non-Newtonian fluids. At very high Ha values, the heat transfer is mainly assured by the conduction regime. Moreover, the temperature-dependent viscosity in MHD results in the disappearance of the Centro symmetry of the central cell and the migration of the center towards the active wall.
Downloads