Modelling 2-D Heat Transfer Problem for Different Material Combination
DOI:
https://doi.org/10.37934/arfmts.111.1.135155Keywords:
Numerical method, programming, modelling heat transfer, optimum grid sizeAbstract
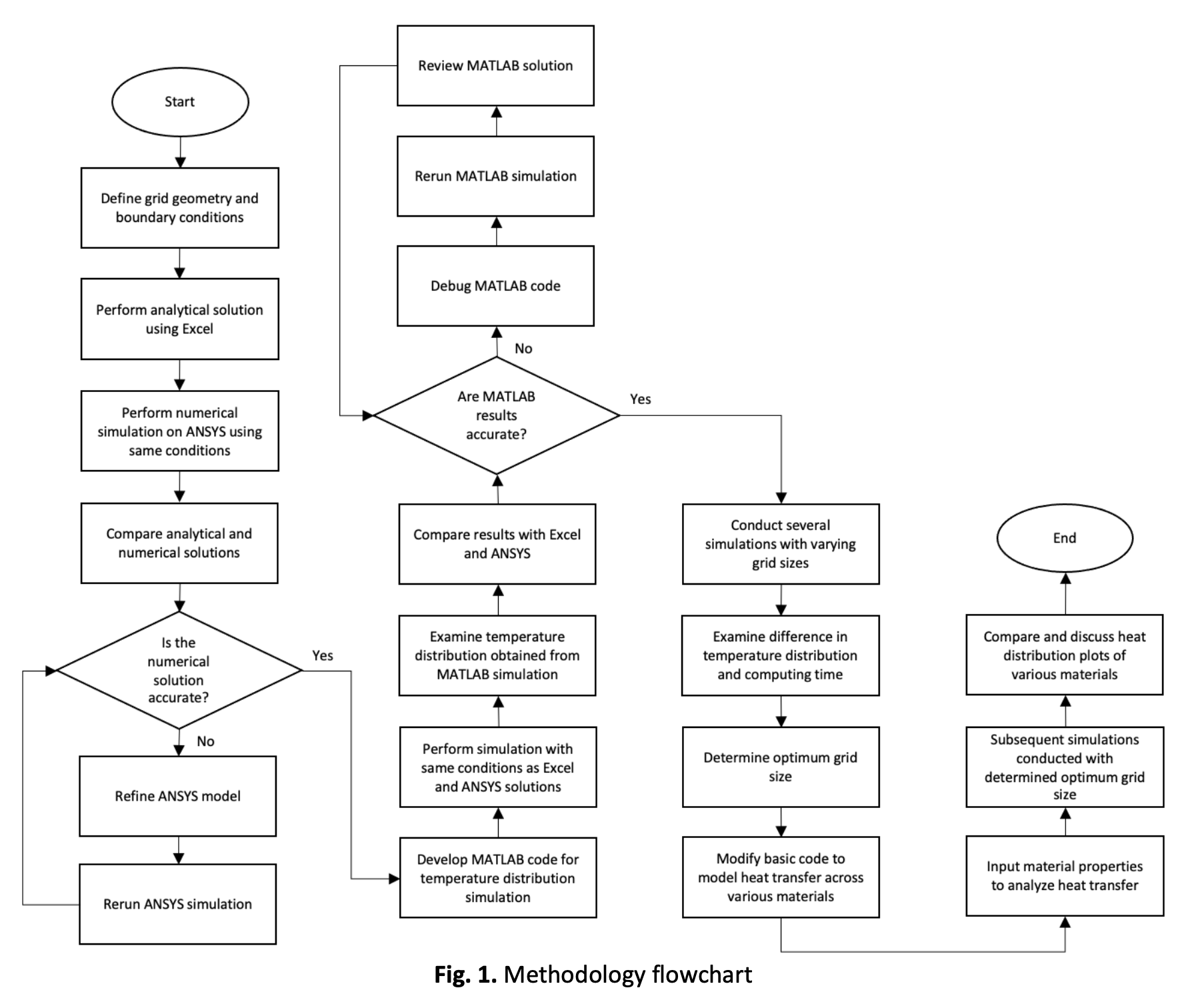
The analysis of heat transfer problems can be highly complex due to factors such as temperature, position, and time. Most heat transfers are typically two-dimensional as conduction is often negligible in the third dimension. Two-dimensional heat conduction problems can be solved analytically or numerically. In steady-state conditions, the Laplace equation can be applied to solve two-dimensional heat conduction problems analytically, in which the separation of variables method is used to solve the Laplace equation under fixed boundary conditions to determine the temperature at a specific point. The Laplace equation plays a significant role in the solution of heat transfer problems, as it demonstrates the behavior of linear and non-linear equations in the computational fluid dynamics domain. Despite their inability to provide exact results at any point, numerical methods are superior to analytical methods when handling complex geometries with various boundary conditions. This project involves the development of a computational code using MATLAB to solve two-dimensional steady-state heat conduction problems using Gauss-Seidel iterations. Comparing analytical solutions from Excel with numerical solutions from MATLAB and ANSYS, specifically the developed MATLAB code, revealed an accuracy level of 99.902% for the Laplace equation. An analysis of the produced code from MATLAB found that it could solve two-dimensional steady-state heat conduction across different combinations of materials while allowing users to specify initial and boundary conditions to produce a contour plot similar to ANSYS.
Downloads