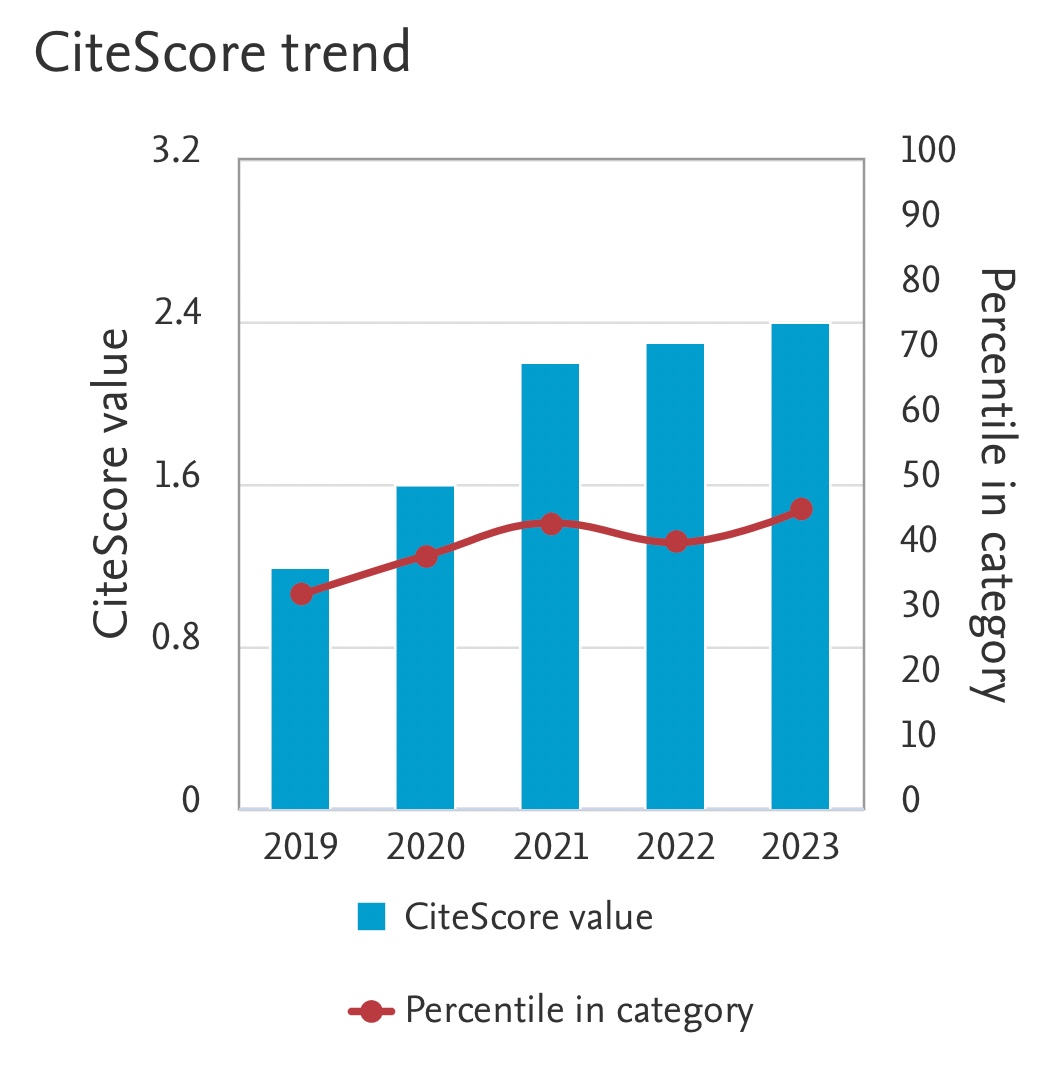
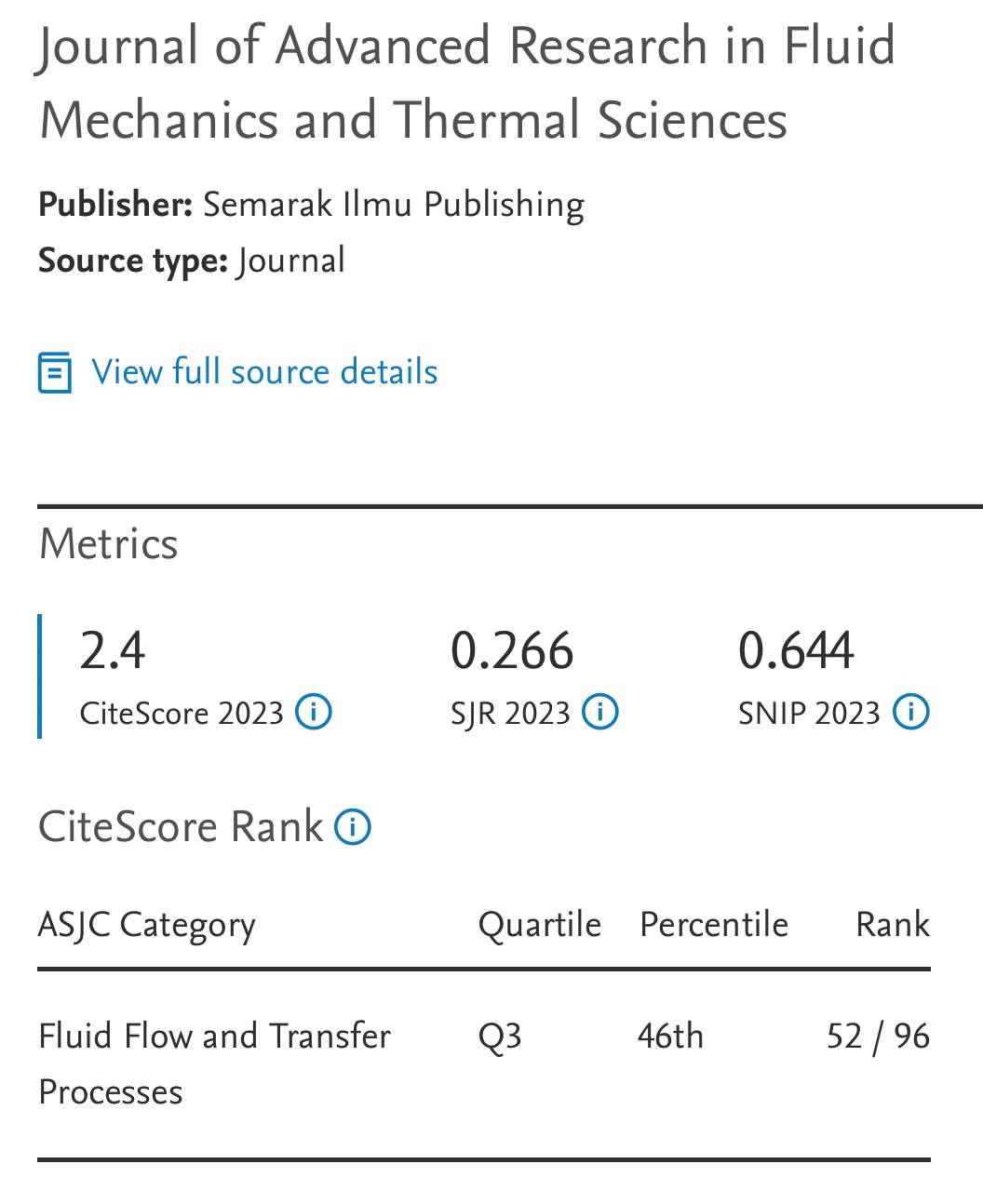
Exact Equilibria for Ideal MHD Plasmas with Helically  Symmetric Incompressible Flows and Variable Gravitational  Field

Salah Moawad; Omar El-Kalaawy; Heba Shaker

Authors

Salah Moawad Department of Mathematics and Computer Science Department, Faculty of Science, Beni-Suef University, Beni-Suef, Egypt
Omar El-Kalaawy Department of Mathematics and Computer Science Department, Faculty of Science, Beni-Suef University, Beni-Suef, Egypt
Heba Shaker Future High Institute of Engineering in Fyoum, Ministry of High Education, Fyoum, Egypt

Keywords:

Fluid dynamics, Helical symmetry, Incompressible flows, Exact equilibria

Abstract

The equilibrium states of the system under consideration are governed by a nonlinear elliptic partial differential equation (PDE) for the helical magnetic flux function containing surface quantities along with a relation for the pressure. This leads to the study of equilibrium equations, which permit the derivation of several classes of analytic solutions with non-constant Mach number and differentially varying electric field perpendicular to the magnetic surfaces. The aim of this paper is the analytical solution of magnetohydrodynamic (MHD) flow. The equilibrium equations of motion for gravitating MHD plasmas are derived in the presence of incompressible mass flows with helical symmetry. The gravitational field is taken to be a variable vector function in a space of a cylindrical coordinates (r, ϕ, z). A similarity reduction approach is used to obtain exact solutions for several cases of the considered plasma flows with variable Mach number.