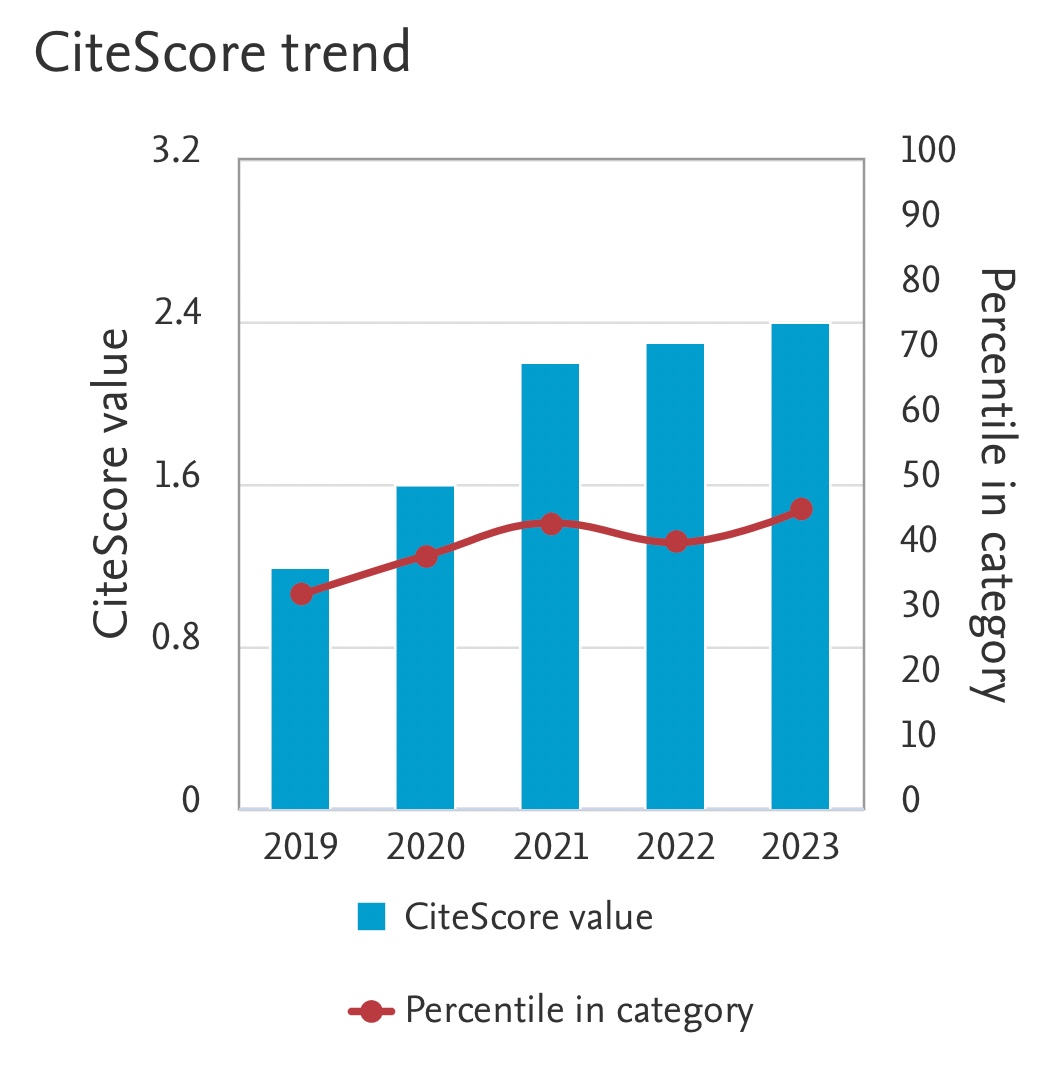
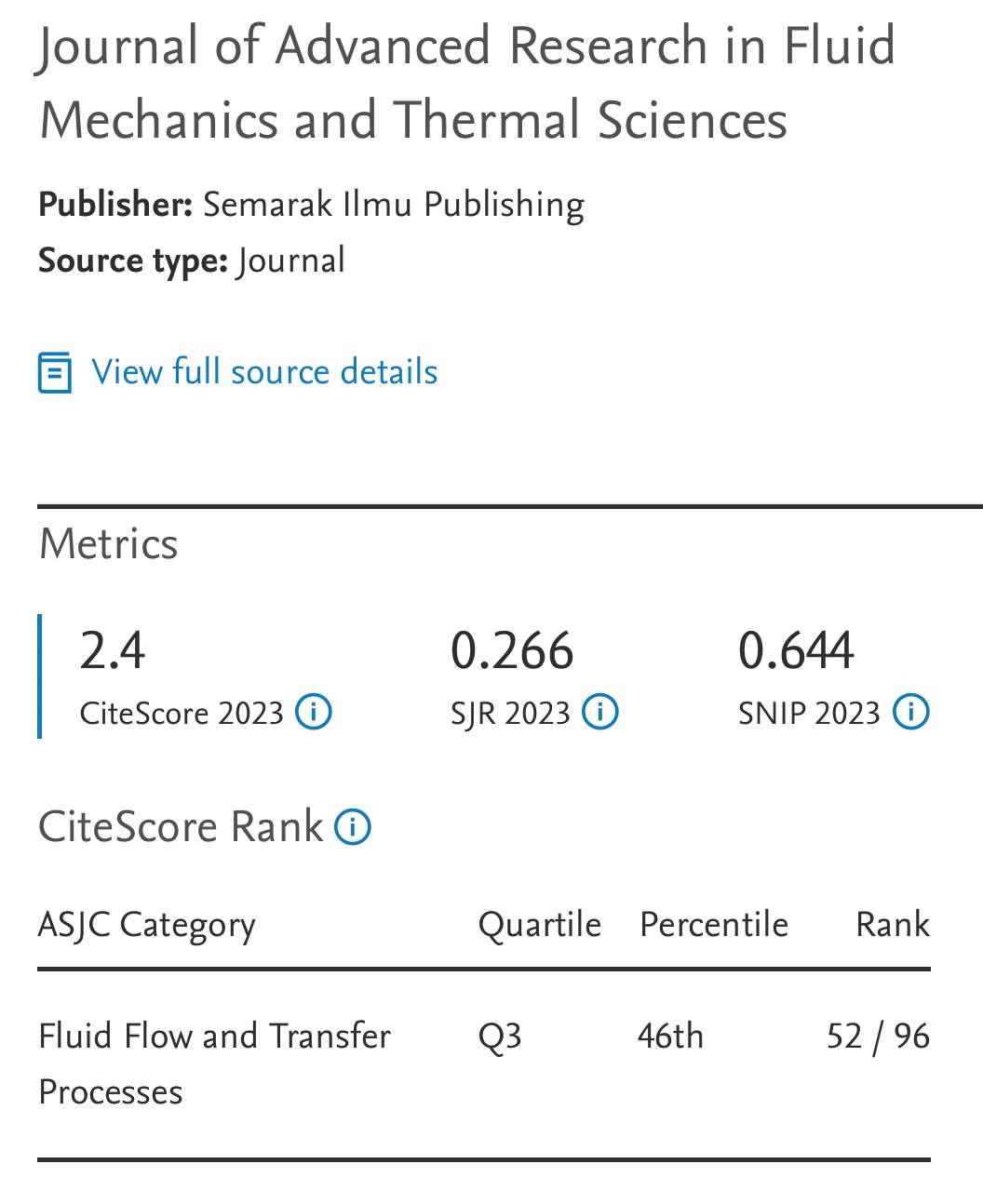
Relaxation Equations of Consolidating Cake Filtration
Keywords:
Cake filtration, filter, relaxation, relaxing cake, Stefan problem, suspensionAbstract
In this paper, on the basis of conservation laws suspensions filtration equations with forming a relaxing cake are derived. The equations are numerically solved. To solve the equation for cake growth a Stefan problem is posed and solved with using the method of catching a moving front. On the basis of numerical results influence of relaxation phenomena on filtration characteristics is established. It is shown that the relaxation slows down the increasing of local filter cake porosity and decreasing of cake permeability, as well as increase fluid relative velocity through cake for given applied pressure. Increasing of relaxation time leads to a faster growth of the cake thickness when all other conditions are constants, thus relaxation effects cause more intensive transfer of particles from suspension to the cake. It, in turn, alters all other filtration characteristics, such as fluid pressure distribution, compressive pressure, porosity and consolidation of the cake, fluid flow rate through the cake and effective hydrodynamic resistance. With increasing of relaxation phenomena dynamics of current and total outlet filtrate flow rate becomes more intensive.
Downloads