Compartmental Equations Hybrid Model for Modelling Water Pollution Transmission
DOI:
https://doi.org/10.37934/arfmts.115.1.3050Keywords:
Water pollutants, mathematical modelling, compartment model, Euler method and Runge-KuttaAbstract
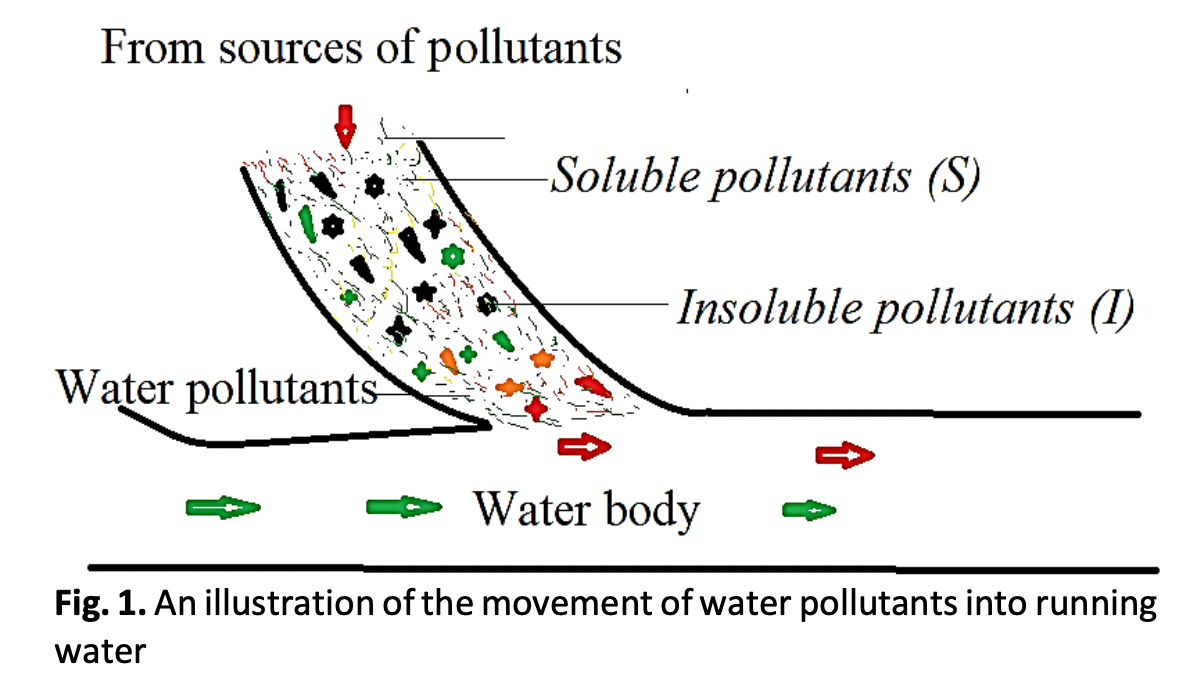
Water pollution has been identified as one of serious environmental problem that has a negative impact on aquatic animals and plants, terrestrial plants and animals, and human health. Effective pollution management and decision-making require an understanding of the intricate dynamics of water contamination in our environment. There are many workable measures that can be adopted to control the menace. Mathematically, water pollution can be modelled using differential equations through management. In order to describe the pollution of water bodies using a system of differential equations. We deployed compartment models to capture the dynamic of pollution in lakes, rivers, and other water bodies. The model compartmentalizes various forms of water pollution and combines them with purification measures. With this strategy, we showed how water pollutants behave in diverse environmental contexts by providing useful knowledge for putting pollution management measures into practice by solving the compartmental model using the Euler method and the Runge-Kutta of Order 4 numerical method (RK4). The quality of results obtained by applying the two mentioned numerical methods is queried based on how they respond to different values of step size (h), which represents the interval at which the numerical methods approximate the solution trajectory. Our findings demonstrate that both numerical approaches are viable for solving compartmental equations by computing compartment values over a specified time interval. Despite the practicability of both methods, it is noteworthy that Runge-Kutta of order 4 consistently emerges as the more effective numerical method in solving our compartmental model when compared with Euler formula, particularly when step sizes are moderately large. The Runge-Kutta method's robustness and efficiency in accurately approximating solutions over the specified time range make us conclude that it is more preferable to the Euler method for practical implementations of compartmental models with moderately large time steps.
Downloads