Solitary Wave Solutions for Forced Nonlinear Korteweg-de Vries Equation by Using Approximate Analytical Method
DOI:
https://doi.org/10.37934/arfmts.99.2.197206Keywords:
Adomian polynomials, Multistep approach, modified Reduced Differential Transform Method, forced NKdV equations, shallow water waves, tsunamiAbstract
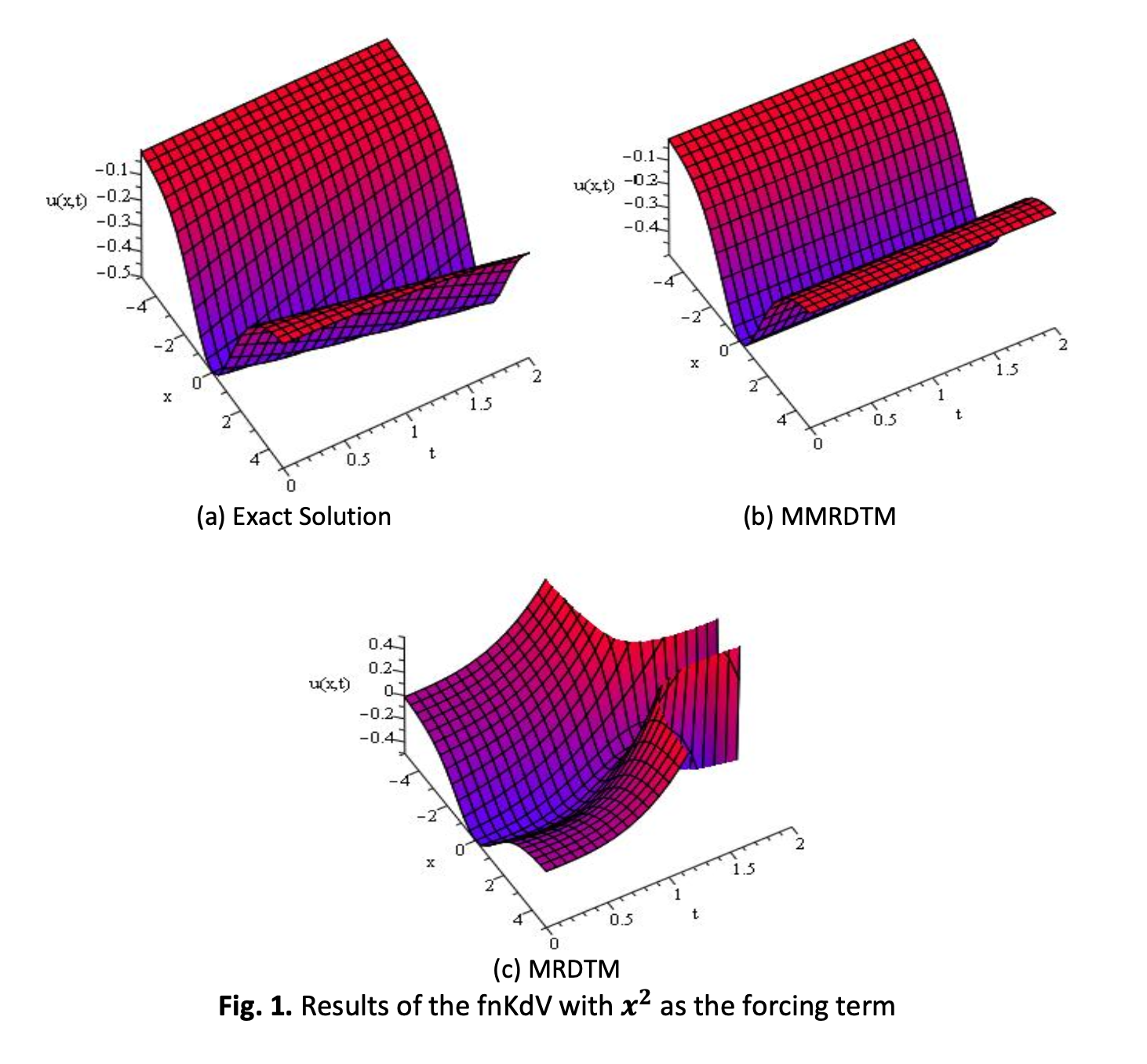
The Multistep Modified Reduced Differential Transform Method (MMRDTM) is proposed in this paper. It is implemented to solve the forced nonlinear Korteweg-de Vries (fnKdV) equations. There are several advantages of the proposed method. Using the suggested approach, a high-speed converging series can be approximated analytically. Furthermore, the number of calculated terms is reduced significantly. The nonlinear term in fnKdV equations is substituted with corresponding Adomian polynomials before applying the multi-step technique. As a result, we provided simpler and more effective ways to solve fnKdV equations. On top of that, the solutions can be approximated more accurately over a longer period of time. To show the MMRDTM's capability and accuracy, we consider several of the fnKdV examples to illustrate the proposed method’s potential in analytical approximation. Then, the features of the solutions are represented in tabular and graphical forms. In conclusion, the proposed method delivers highly accurate and precise solutions for these types of equations.
Downloads