Identifying Irregular Rainfall Patterns Using Persistent Homology

Abstract

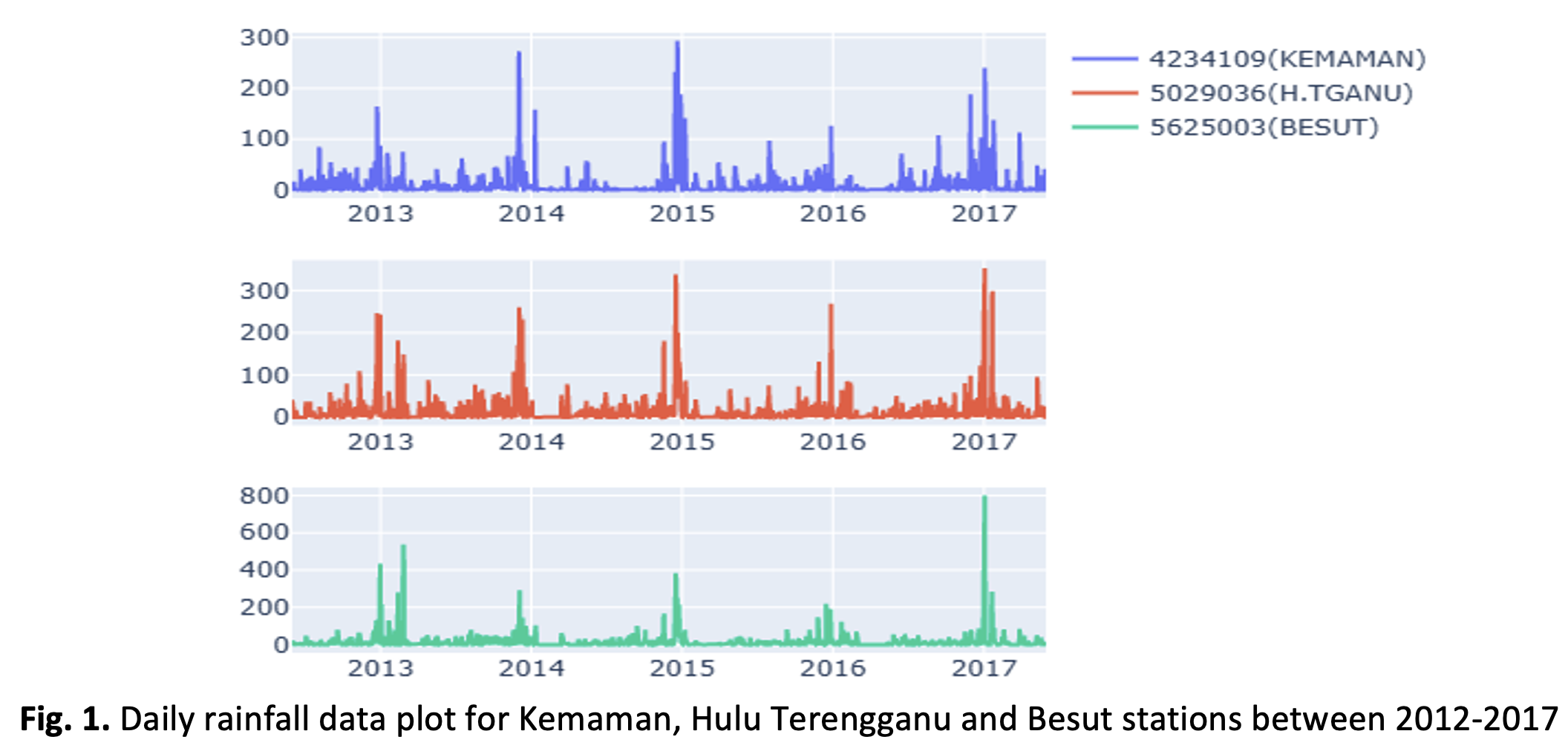
Efficient investigation tools are required to elucidate the changes in climatic change caused by various climate processes, variables, and socioeconomic development activities around the world. In this study, we track the changes of daily rainfall at three flood-prone sites in Terengganu between 2012 to 2017. In recent years, topological data analysis (TDA) has been applied in many fields of data analytics to rank, classify, and cluster time series datasets. In this work, we employ Persistent Homology to quantify and identify topological patterns from a rainfall data. A sliding window (SW) approach is used for each 1D rainfall dataset to embed in higher dimensions before computing its Persistence Diagrams (PD). The topological information obtained from PD, namely connected components (H₀) is then retrieved and vectorized in the form of Persistence Curves (Persistence Landscape (PL), Persistence lifetime Curve (PLC), and Persistence Lifetime Entropy (PLE)) to identify unusual rainfall patterns. We employ various types of L₁-norms from these Persistence vectors to identify anomalies in rainfall data which can be used as an early warning flood system. The irregular pattern of Persistence lifetime and Persistence entropy mismatch the actual flood events suggesting that the irregular points may not be as closely related to flood risk. However, PL analysis of the irregular points shows match of about 59% to the flood events.It is expected that other determining factors, for example, land use, cloud cover, and wind information, which can be obtained via satellite gridded data may increase the predictability of flood events thus promotes an effective flood risk management strategies.