Clustering Datasaurus Dozen Using Bottleneck Distance, Wasserstein Distance (WD) and Persistence Landscapes

Abstract

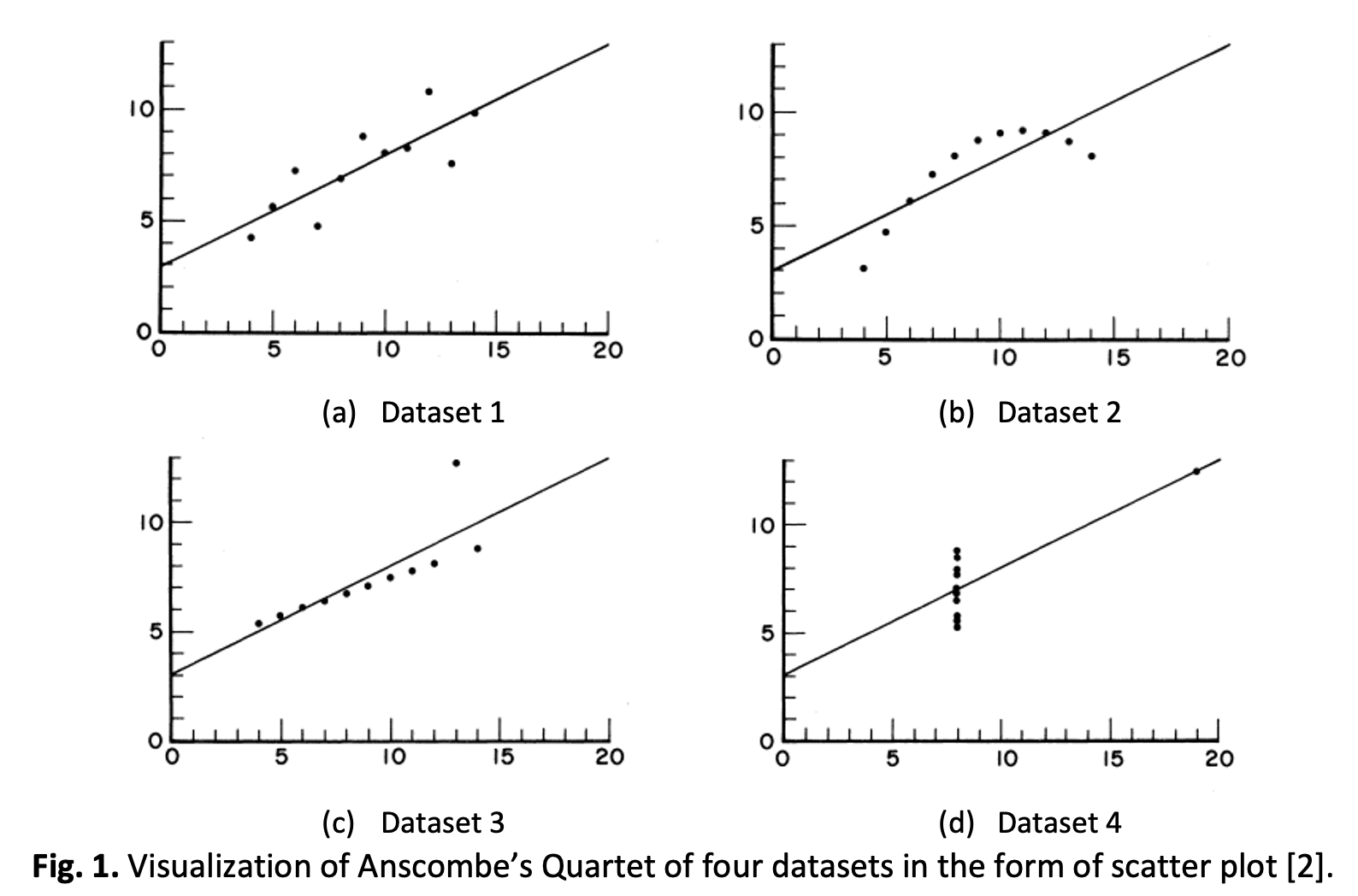
Topological Data Analysis (TDA) is an emerging field of study that helps to obtain insights from the topological information of datasets. Motivated by the emergence of TDA, we applied Persistent Homology (PH), one of the tools commonly used to extract topological features to cluster the Datasaurus Dozen dataset. This dataset is ideal to show PH’s capability in clustering as it consists of twelve distinct point clouds (PC) that have identical mean values, standard deviation, and correlation values, yet produce dissimilar patterns. The methodology starts with normalizing Datasaurus Dozen, followed by computing H₁ Persistence Diagrams (PD) for each dataset. Two types of PD distances are computed directly: Wasserstein Distance (WD) and Bottleneck Distance (BD) and represented as proximity matrix. We also vectorized H₁ Persistence Diagrams to obtain the average of first five strips of Persistence Landscape (PL) and computed L₂ distance to represent a proximity matrix. These three distance matrices are used to generate dendrograms by using Hierarchical Agglomerative Clustering (HAC). Regardless of possessing similar descriptive statistics, PH accurately extracts the global and local geometric topological information, and clusters them accordingly. It is evident that for clustering based on global geometric information, BD is suitable and computably cheap, whereas for clustering based on local geometric information, WD and average PL vectors are suitable but may incur extra computation.