New Analytical Study of Heat Transfer Analysis of Jeffery–Hamel Nanofluid Flow Problem with Porous Medium

Abstract

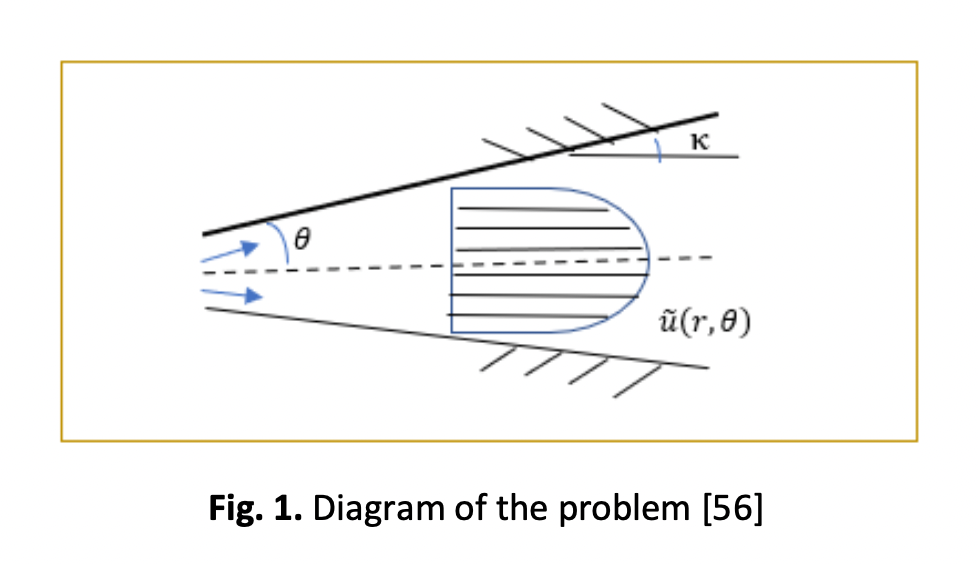
In this study, a perturbation iteration scheme (PIS), is used to investigate the flow and heat transfer of a nanofluid through a convergent or divergent channel in a porous medium for the Jeffrey Hamel flow problem. Under the influence of the magnetic field, the nanofluid continuously flows through the channel. Modeling of the motion of different nanofluids is done with the aid of momentum and energy equations. The effect of some variables such as opening channel angle, Reynolds number, Darcy number, Hartmann number, Prandtl number, and Eckert number, on nanofluidic flows through non-parallel plates has been discussed. It has been observed that as velocity rises, fluid viscosity increases with a higher Reynolds number. The internal friction also decreases as the Darcy number rises because of an increase in flow and an increase in heat transfer. Additionally, when the results of the remaining variables were examined and their effects on the velocity and temperature profiles were compared with those of related studies in the literature, a satisfactory level of agreement was found. This is clear from the tables and drawings mentioned in this manuscript, and it also shows that this approach gives us a good study for examining the Jeffrey Hamel problem.