Improve Solutions of Differential Transform Method for Jeffrey Hamel Magneto-hydrodynamic Non-Newtonian Casson Fluid Flow Problem

Abstract

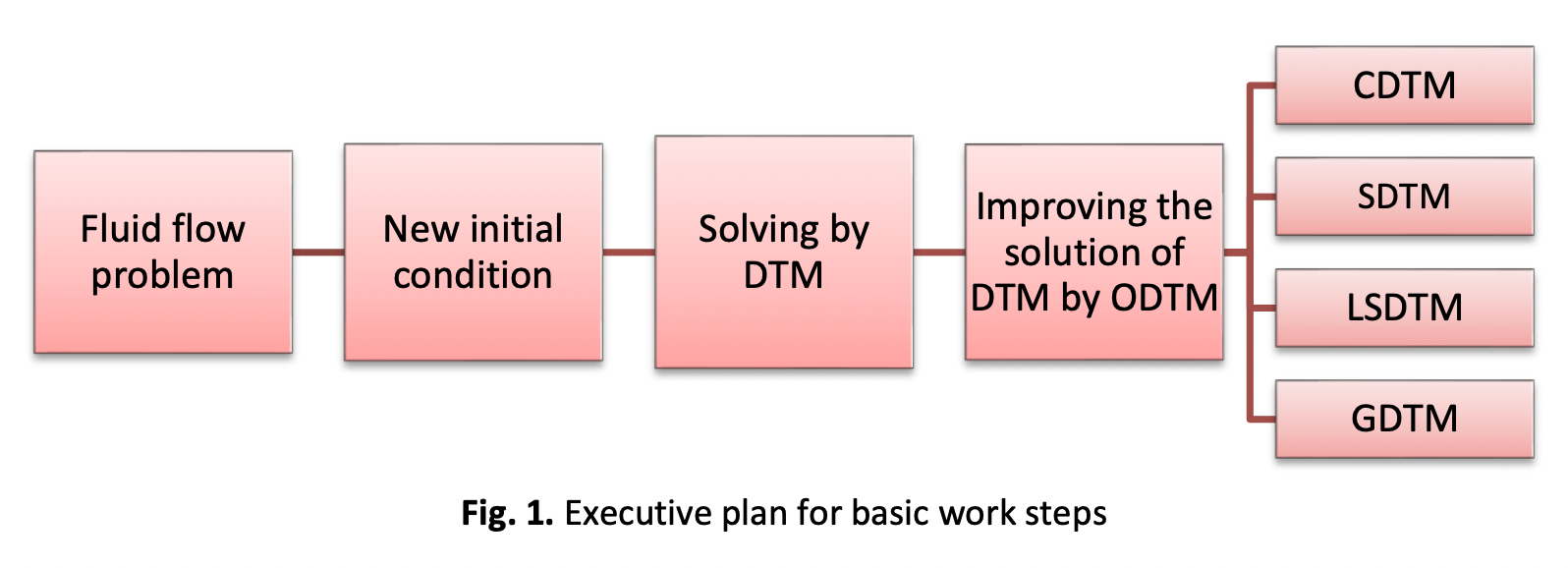
In this article, Magneto-hydrodynamic flow of a non-Newtonian Casson fluid in converging and diverging channels subject to stretching -shrinking cases is an important problem in the field of fluid flow that has been highlighted by the combination of the differential transformation method and the optimal method so-called optimal differential transformation method (ODTM). In this synthesis that is used achieves improved analytical results for this problem. This study examines the impact of several developing characteristics, including channel angle, stretching-shrinking parameter, Casson fluid parameter, Hartmann number, and Reynolds number with the velocity profiles. Results obtained from the DTM and the numerical method BVP4c are compared to those resulting from ODTM which consist of the collocation differential transform method (CDTM), the sub-domain differential transform method (SDTM), the least squares differential transform method (LSDTM), and the Galerkin differential transform method (GDTM). The comparison shows that the percentage errors of the optimal methods (ODTM) are more accurate than those of the DTM for a similar number of parts of the repeated series over a wide range of physical parameters. Finally, it can be said that the results of the proposed method for third-order nonlinear Jeffrey Hamel flow in the non-Newtonian Casson fluid problem are high accuracy.