Numerical Solution of Darcy-Forchheimer Casson Nanofluid Flows with Joule Heating and Radiation

Abstract

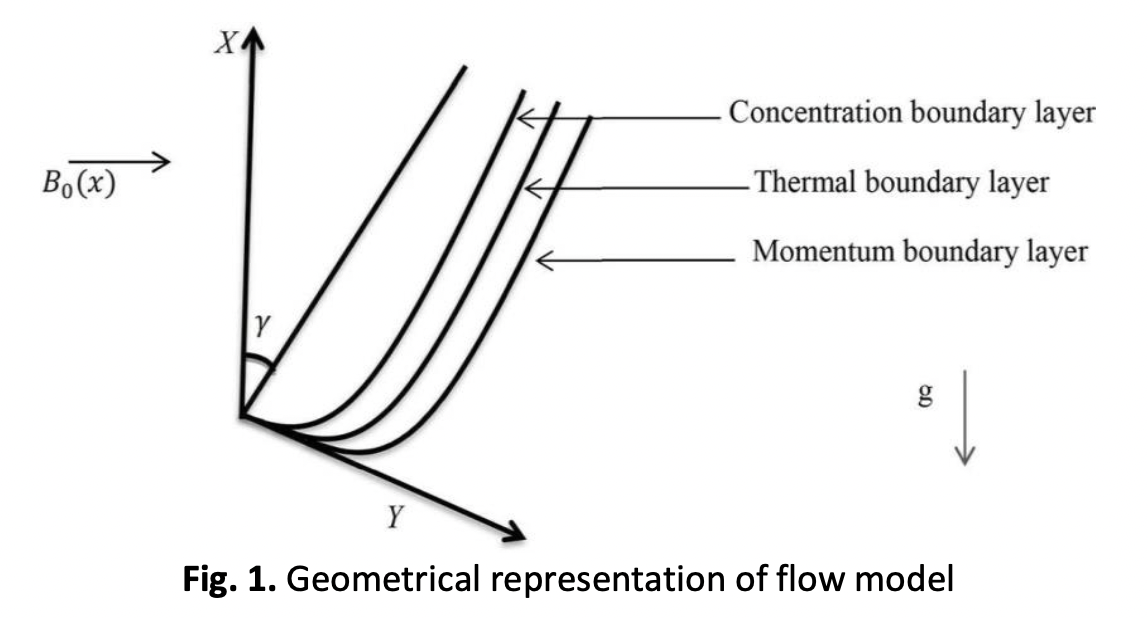
The present article provides a description of the hydrothermal properties of a Non –Newtonian nanofluid flow over a Darcy surface that is undergoing extension. The Darcy-Forchheimer effect is a phenomenon that describes the movement of nanofluids through a variable surface. The present study aims to investigate the impact of thermal radiation on heat transfer in magnetohydrodynamic (MHD) flow, utilizing a Casson nanofluid. The impacts of chemical reaction, magnetic field and thermal radiation are taken into consideration. The flow equations are transformed to ordinary differential equations by the appropriate similarity transformations. The Keller-Box method is used to compute the governing differential equations. It is found that the angle of inclination parameter enhances the thermal boundary layer thickness of the flow and the Joule heating parameter improves the thermal boundary layer thickness and slows the fluid velocity, which helps to maintain system temperature. The rate of Heat is increasing while mass transfer rate decreasing with the increasing values Brownian motion. Numerical and graphical results of various flow parameters as well as heat and mass rates are also provided in tables and graphs. So, the observation of the results systems for electronic devices, where the interaction of fluid flow, heat transfer, and electromagnetic effects is significant.