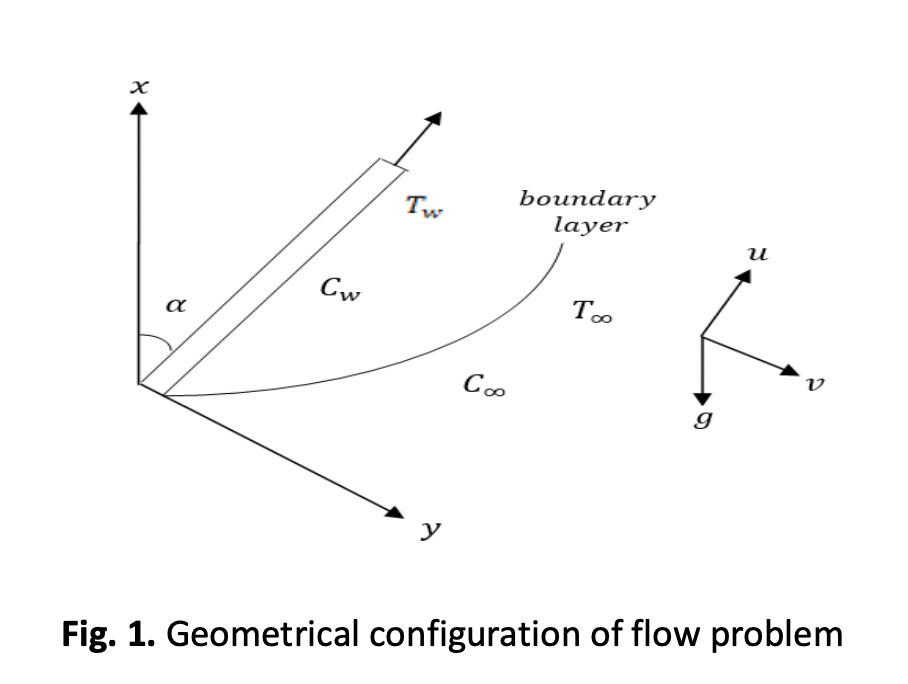
Flow And Heat Transfer of Unsteady Two-Phase Boundary Layer Flow Past an Inclined Permeable Stretching Sheet with Electrification of Particles
DOI:
https://doi.org/10.37934/cfdl.15.5.134144Keywords:
Two-phase Flow, Stretching Sheet, Similarity transformationAbstract
In the present study, an analysis has been carried out for a particle laden boundary layer flow with existence of electrification of particles has been studied over an inclined permeable stretching sheet. In most of the MHD fluid flow problems, either the plate is externally supplied by the magnetic/electric field or the fluid is electrically conducting. In the present problem, neither the plate is electrified nor the fluid is electrically conducted, but due to the random motion of the particles, collision of particle-particle and particle–wall, the particles are electrified. This electric field affects the fluid flow and heat transfer of the flow problem. Again, in the previous literatures, Buoyancy force is considered in momentum equations of fluid phase only. But in reality, both the phases are affected by the buoyancy force. For this reason, a reasonable mathematical model for two-phase buoyancy driven flow has been formulated with the consideration of electrification of particles in both fluid and particle phase. The governing system of PDEs are transferred to system of ODEs by applying similarity transformations and then computed by implementing Runga-Kutta method. The impact of electrification and other fluid parameters on flow and heat transfer has been studied. The results are represented through graphs and tables
Downloads
References
Kanungo, Subhrajit, and Tumbanath Samantara. "Numerical Solution of Two-Phase Radiated Unsteady Flow Over a Horizontal Stretching Sheet with Simultaneous Effect of Electrification, Radiation and Non-Uniform Internal Heat Source/Sink." Journal of Advanced Research in Fluid Mechanics and Thermal Sciences 100, no. 3 (2022): 11-22. https://doi.org/10.37934/arfmts.100.3.1122
Grubka, L. J., and K. M. Bobba. "Heat transfer characteristics of a continuous stretching surface with variable temperature." Journal of Heat Transfer 107, no. 1 (1985): 248-250. https://doi.org/10.1115/1.3247387
Sharidan, S., M. Mahmood, and I. Pop. "Similarity solutions for the unsteady boundary layer flow and heat transfer due to a stretching sheet." Applied Mechanics and Engineering 11, no. 3 (2006): 647.
Chen, C-H. "Laminar mixed convection adjacent to vertical, continuously stretching sheets." Heat and Mass transfer 33, no. 5 (1998): 471-476.. https://doi.org/10.1007/s002310050217
Rashidi, Mohammad Mehdi, Behnam Rostami, Navid Freidoonimehr, and Saeid Abbasbandy. "Free convective heat and mass transfer for MHD fluid flow over a permeable vertical stretching sheet in the presence of the radiation and buoyancy effects." Ain Shams Engineering Journal 5, no. 3 (2014): 901-912. https://doi.org/10.1016/j.asej.2014.02.007
Hady, F. M., R. A. Mohamed, and Hillal M. ElShehabey. "Thermal Radiation, Heat Source/Sink and Work Done by Deformation Impacts on MHD Viscoelastic Fluid over a Nonlinear Stretching Sheet." World Journal of Mechanics 3, no. 04 (2013): 203. https://doi.org/10.4236/wjm.2013.34020
Mukhopadhyay, Swati, and Helge I. Andersson. "Effects of slip and heat transfer analysis of flow over an unsteady stretching surface." Heat and Mass Transfer 45, no. 11 (2009): 1447-1452.. https://doi.org/10.1007/s00231-009-0516-7
Machireddy, Gnaneswara Reddy, and Sandeep Naramgari. "Heat and mass transfer in radiative MHD Carreau fluid with cross diffusion." Ain Shams Engineering Journal 9, no. 4 (2018): 1189-1204. https://doi.org/10.1016/j.asej.2016.06.012
Tripathy, Pradeep Kumar, Tumbanath Samantara, Jayaprakash Mishra, and Sujata Panda. "Mixed convective radiative heat transfer in a particle-laden boundary layer fluid over an exponentially stretching permeable surface." In AIP Conference Proceedings, vol. 2435, no. 1, p. 020030. AIP Publishing LLC, 2022. https://doi.org/10.1063/5.0083840
Samantara, Tumbanath. “Velocity profile of fluid particle suspension over a horizontal plate with electrification of particles.”International Journal of Innovative Technology and Exploring Engineering 8, no. 11 (2019): 1119-1122. https://doi.org/10.35940/ijitee.J1220.0981119
Samantara, Tumnanath, S. K. Mishra, and T. C. Panda. "Numerical Modeling of Two Phase Jet Flow and Heat Transfer with Charged Suspended Particulate Matter (SPM)." Modelling, Measurement and Control B 86: 885-906. https://doi.org/10.18280/mmc_b.860405
Samantara, Tumnanath, S. K. Mishra, and T. C. Panda. "Numerical Modeling of Two Phase Jet Flow and Heat Transfer with Charged Suspended Particulate Matter (SPM)." Modelling, Measurement and Control B 86: 885-906. https://doi.org/10.18280/mmc_b.860405
Ishak, Anuar, Roslinda Nazar, and I. Pop. "Hydromagnetic flow and heat transfer adjacent to a stretching vertical sheet." Heat and Mass Transfer 44, no. 8 (2008): 921-927. https://doi.org/10.1007/s00231-007-0322-z
Abel, M. Subhas, and N. Mahesha. "Heat transfer in MHD viscoelastic fluid flow over a stretching sheet with variable thermal conductivity, non-uniform heat source and radiation." Applied Mathematical Modelling 32, no. 10 (2008): 1965-1983. https://doi.org/10.1016/j.apm.2007.06.038
Gireesha, B. J., A. J. Chamkha, S. Manjunatha, and C. S. Bagewadi. "Mixed convective flow of a dusty fluid over a vertical stretching sheet with non‐uniform heat source/sink and radiation." International Journal of Numerical Methods for Heat & Fluid Flow 23, no. 4 (2013): 598-612. https://doi.org/10.1108/09615531311323764