Control Effect on Rayleigh-Benard Convection in Rotating Nanofluids Layer with Double-Diffusive Coefficients
DOI:
https://doi.org/10.37934/cfdl.14.3.7995Keywords:
Nanofluids, rotation, feedback control, double-diffusive coefficientsAbstract
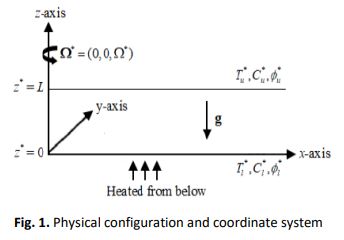
Rayleigh-Benard convection in rotating nanofluids layer with feedback control and double-diffusive coefficients heated from below is examined. The model for nanofluid includes the mechanism of Brownian motion and thermophoresis. The system is considered for three types of lower-upper boundary conditions, free-free, rigid-free and rigid-rigid. Linear stability analysis based on normal mode technique is employed, the eigenvalue solution is obtained by Galerkin technique and solved by using Maple software. The effects of rotation, feedback control, double-diffusive cofficients and nanofluids parameters have significant impact to the system. Based on the observation, the effect of increasing the value of rotation, feedback control, Dufour parameter and solutal Rayleigh number are observed to stabilize the system. Meanwhile, the effect of increasing the value of Soret parameter, nanofluids Lewis number, nanoparticles concentration Rayleigh number and modified diffusivity ratio are found to destabilize the system. The effect of modified particles density increment in the system is very small and can be neglected. The effects of the parameters in the system are discussed and presented graphically.
Downloads
References
Choi, S. US, and Jeffrey A. Eastman. Enhancing thermal conductivity of fluids with nanoparticles. No. ANL/MSD/CP-84938; CONF-951135-29. Argonne National Lab.(ANL), Argonne, IL (United States), 1995.
Masuda, Hidetoshi, Akira Ebata, Kazunari Teramae, and N. Hishiunma. "conductivity and viscosity of liquid by dispersed ultra-fine particles (dispersion of Al2O3, SiO2, and TiO2 ultra-fine particles)." Alteration of Thermal, Netsu Bussei (Japan) 7, no. 4 (1993): 227-233. https://doi.org/10.2963/jjtp.7.227
Xuan, Yimin, and Qiang Li. "Heat transfer enhancement of nanofluids." International Journal of heat and fluid flow 21, no. 1 (2000): 58-64. https://doi.org/10.1016/S0142-727X(99)00067-3
Eastman, Jeffrey A., S. U. S. Choi, Sheng Li, W. Yu, and L. J. Thompson. "Anomalously increased effective thermal conductivities of ethylene glycol-based nanofluids containing copper nanoparticles." Applied physics letters 78, no. 6 (2001): 718-720. https://doi.org/10.1063/1.1341218
Das, S. K., N. Putra, P. Thiesen, and W. Roetzel. "†œTemperature dependence of thermal conductivity enhancement for nanofluids, †J." Heat Transf 125 (2003): 567-574. https://doi.org/10.1115/1.1571080
Menni, Younes, Ali J. Chamkha, and Houari Ameur. "Advances of nanofluids in heat exchangers—A review." Heat Transfer 49, no. 8 (2020): 4321-4349. https://doi.org/10.1002/htj.21829
Buongiorno, Jacopo. "Convective transport in nanofluids." Journal of Heat Transfer 128, no. 3 (2006): 240-250. https://doi.org/10.1115/1.2150834
Farhana, K., K. Kadirgama, D. Ramasamy, M. Samykano, and G. Najafi. "Experimental Studies on Thermo-Physical Properties of Nanocellulose–Aqueous Ethylene Glycol Nanofluids." Journal of Advanced Research in Materials Science 69, no. 1 (2020): 1-15. https://doi.org/10.37934/arms.69.1.115
Tzou, DY1143. "Instability of nanofluids in natural convection." Journal of Heat Transfer 130, no. 7 (2008): 1-9. https://doi.org/10.1115/1.2908427
Tzou, Da Yu. "Thermal instability of nanofluids in natural convection." International Journal of Heat and Mass Transfer 51, no. 11-12 (2008): 2967-2979. https://doi.org/10.1016/j.ijheatmasstransfer.2007.09.014
Nield, D. A., and Andrey V. Kuznetsov. "The onset of convection in a horizontal nanofluid layer of finite depth." European Journal of Mechanics-B/Fluids 29, no. 3 (2010): 217-223. https://doi.org/10.1016/j.euromechflu.2010.02.003
Yadav, D., Agrawal, G. S., and Bhargava, R. "Rayleigh-Benard convection in nanofluids." International Journal of Applied Mathematics and Mechanics 7, no. 2 (2011): 61-76.
Haddad, Z., Abu-Nada, E., Oztop, H. F., and Mataoui, A. "Natural convection in nanofluids: Are the thermophoresis and Brownian motion effects significant in nanofluids heat transfer enhancement?" International Journal of Thermal Sciences 57, (2012): 152-162. https://doi.org/10.1016/j.ijthermalsci.2012.01.016
Douha, Mohammed, Draoui Belkacem, Kaid Noureddine, Ameur Houari, Belkacem Abdellah, Mohamed Elmir, Merabti Abdelhak, and Aissani Houcine. "Study of Laminar Naturel Convection in Partially Porous Cavity in the Presence of Nanofluids." Journal of Advanced Research in Fluid Mechanics and Thermal Sciences 79, no. 1 (2021): 91-110. https://doi.org/10.37934/arfmts.79.1.91110
Aliouane, Imane, Noureddine Kaid, Houari Ameur, and Houssem Laidoudi. "Investigation of the flow and thermal fields in square enclosures: Rayleigh-Bénard’s instabilities of nanofluids." Thermal Science and Engineering Progress 25 (2021): 100959. https://doi.org/10.1016/j.tsep.2021.100959
Mahammedi, Abdelkader, Houari Ameur, Younes Menni, and Driss Meddah Medjahed. "Numerical study of turbulent flows and convective heat transfer of Al2O3-water nanofluids in a circular tube." Journal of Advanced Research in Fluid Mechanics and Thermal Sciences 77, no. 2 (2021): 1-12. https://doi.org/10.37934/arfmts.77.2.112
Abdelkader, Mahammedi, Houari Ameur, and Younes Menni. "Investigation of the convective heat transfer and friction factor of magnetic Ni nanofluids within cylindrical pipes." transfer 2 (2021): 4. https://doi.org/10.36963/IJTST.2021080101
Phu, Nguyen Minh, Pham Ba Thao, and Duong Cong Truyen. "Heat and fluid flow characteristics of nanofluid in a channel baffled opposite to the heated wall." CFD Letters 13, no. 1 (2021): 33-44. https://doi.org/10.37934/cfdl.13.1.3344
Azman, Azraf, Mohd Zamri Yusoff, Azfarizal Mukhtar, Prem Gunnasegaran, Nasri A. Hamid, and Ng Khai Ching. "Numerical Study of Heat Transfer Enhancement for Mono and Hybrid Nanofluids Flow in a Straight Pipe." CFD Letters 13, no. 2 (2021): 49-61. https://doi.org/10.37934/cfdl.13.2.4961
Hurle, D. T. J., and E. Jakeman. "Soret-driven thermosolutal convection." Journal of Fluid Mechanics 47, no. 4 (1971): 667-687. https://doi.org/10.1017/S0022112071001319
Platten, J. K., and G. Chavepeyer. "Oscillatory motion in Bénard cell due to the Soret effect." Journal of Fluid Mechanics 60, no. 2 (1973): 305-319. https://doi.org/10.1017/S0022112073000182
Caldwell, D. R. "Non-linear effects in a Rayleigh–Bénard experiment." Journal of Fluid Mechanics 42, no. 1 (1970): 161-175. https://doi.org/10.1017/S0022112070001155
Knobloch, E., and D. R. Moore. "Linear stability of experimental Soret convection." Physical review A 37, no. 3 (1988): 860-870. https://doi.org/10.1103/physreva.37.860
Nield, D. A., and A. V. Kuznetsov. "The onset of double-diffusive convection in a nanofluid layer." International Journal of Heat and Fluid Flow 32, no. 4 (2011): 771-776. https://doi.org/10.1016/j.ijheatfluidflow.2011.03.010
Chand, Ramesh, and Gian Chand Rana. "Magneto convection in a layer of nanofluid with soret effect." acta mechanica et automatica 9, no. 2 (2015): 63-69. https://doi.org/10.1515/ama-2015-0011
Akbar, Noreen, and S. Nadeem. "Double-diffusive natural convective boundary-layer flow of a nanofluid over a stretching sheet with magnetic field." International Journal of Numerical Methods for Heat & Fluid Flow 26, no. 1 (2016): 108-121. https://doi.org/10.1108/HFF-01-2015-0019
Abdulwahab, Mohammed Raad, Nor Azwadi Che Sidik, Siti Nurul Akmal Yusof, and Muhammad Mahmud Jamil. "Magnetic Nanofluids for Heat Transfer Enhancement Inside Straight Channels." Journal of Advanced Research in Materials Science 68, no. 1 (2020): 8-19. https://doi.org/10.37934/arms.68.1.819
Chandrasekhar, S. "Hydrodynamic and hydromagnetic stability." New York: Dover Publication (1961).
Namikawa, T., Takashima, M., and Matsushita, S. "The effect of rotation on convective instability induced by surface tension and buoyancy." Journal of Physical Society of Japan 28, no. 5 (1970): 1340-1349. https://doi.org/10.1143/JPSJ.28.1340
Sunil, Chand, P., Bharti, P. K., and Mahajan, A. "Thermal convection in micropolar ferrofluid in the presence of rotation." Journal of Magnetism and Magnetic Materials 320, no. 3 (2008): 316-324. https://doi.org/10.1016/j.jmmm.2007.06.006
Hirano, T., Guo, Z., and Kirk, R. G. "Application of computational fluid dynamics analysis for rotating machinery-part II: Labyrinth seal analysis.” Journal of Engineering Gas Turbines and Power 127, no. 4 (2005): 820-826. https://doi.org/10.1115/1.1808426
Combescure, D., and Lazarus, A. "Refined finite element modelling for the vibration analysis of large rotating machines: application to the gas turbine modular helium reactor power conversion unit." Journal of Sound and Vibration 381, no. 4-5 (2008): 1261-1280. https://doi.org/10.1016/j.jsv.2008.04.025
Roy, P., Anand, N. K., and Banerjee, D. "Numerical simulation of flow and heat transfer in radially rotating microchannels." Microfluid Nanofluid 15, (2013): 397-413. https://doi.org/10.1007/s10404-013-1159-z
Yadav, D., Agrawal, G. S., and Bhargava, R. "Thermal instability of rotating nanofluid layer." International Journal of Engineering Science 49, no. 11 (2011): 1171-1184. https://doi.org/10.1016/j.ijengsci.2011.07.002
Yadav, D., Agrawal, G. S., and Bhargava, R. "Numerical solution of a thermal instability problem in a rotating nanofluid layer." International Journal of Heat and Mass Transfer 63, (2013): 313-322. https://doi.org/10.1016/j.ijheatmasstransfer.2013.04.003
McConaghy, G. A., and Finlayson, B. A. "Surface tension driven oscillatory instability in a rotating fluid layer." Journal of Fluid Mechanics 39, no. 1 (1969): 49-55. https://doi.org/10.1017/S0022112069002035
Takshima, M., and Namikawa, T. "Surface-tension-driven convection under the simultaneous action of a magnetic field and rotation." Physics Letter A 37, no. 1 (1971): 55-56. https://doi.org/10.1016/0375-9601(71)90329-X
Friedrich, R., and Rudraiah, N. "Marangoni convection in a rotating fluid layer with non-uniform temperature gradient." International Journal of Heat and Mass Transfer 27, no. 3 (1984): 443-449. https://doi.org/10.1016/0017-9310(84)90291-6
Douiebe, A., Hannaoui, M., Lebon, G., Benaboud, A., and Khmou, A. "Effect of a.c. electric field and rotation on Benard-Marangoni convection." Flow, Turbulence and Combustion 67, no. 3 (2001): 185-204. https://doi.org/10.1023/A:1015038222023
Namikawa, T., Takashima, M., and Matsushita, S. "The effect of rotation on convective instability induced by surface tension and buoyancy." Journal of Physical Society of Japan 28, no. 5 (1970): 1340-1349. https://doi.org/10.1143/JPSJ.28.1340
Kaddame, A., and Lebon, G. "Benard-Marangoni convection in a rotating fluid with and without surface deformation." Applied Scientific Research 52, (1970): 295-308. https://doi.org/10.1007/BF00936834
Yadav, D., Bhargava, R., Agrawal, G. S., Hwang, G. S., Lee, J., and Kim, M. C. "Magneto-convection in a rotating layer of nanofluid." Asia-Pacific Journal of Chemical Engineering 9, no. 5 (2014): 663-677. https://doi.org/10.1002/apj.1796
Yadav, D., Agrawal, G. S., and Lee, J. "Thermal instability in a rotating nanofluid layer: a revised model." Ain Shams Engineering Journal 7, no. 1 (2016): 431-440. https://doi.org/10.1016/j.asej.2015.05.005
Tang, J., and Bau, H. H. "Stabilization of the no-motion state in Rayleigh-Benard convection through the use of feedback control." Physical Review A 70, no. 12 (1993a): 1795-1798. https://doi.org/10.1103/PhysRevLett.70.1795
Tang, J., and Bau, H. H. "Feedback control stabilization of the no-motion state of a fluid confined in a horizontal porous layer heated from below." Journal of Fluid Mechanics 257, (1993b): 485-505. https://doi.org/10.1017/S0022112093003179
Tang, J., and Bau, H. H. "Stabilization of the no-motion state of a horizontal fluid layer heated from below with Joule heating." Journal of Heat Transfer 117, no. 2(1995): 329-333. https://doi.org/10.1115/1.2822525
Tang, J., and Bau, H. H. "Experiments on the stabilization of the no-motion state of a fluid layer heated from below and cooled from above." Journal of Fluid Mechanics 363, (1998a): 153-171. https://doi.org/10.1017/S0022112098008891
Tang, J., and Bau, H. H. "Numerical investigation of the stabilization of the no-motion state of a fluid layer heated from below and cooled from above." Physics of Fluids 10, no. 7 (1998b): 1597-1610. https://doi.org/10.1063/1.869679
Howle, L. E. "Control of Rayleigh-Benard convection in a small aspect ratio container." International Journal of Heat and Mass Transfer 40, no. 4 (1997a): 817-822. https://doi.org/10.1016/0017-9310(96)00174-3
Howle, L. E. "Active control of Rayleigh-Benard convection." Physics of Fluids 9, no. 7 (1997b): 1861-1863. https://doi.org/10.1063/1.869335
Howle, L. E. "Linear stability analysis of controlled Rayleigh-Benard convection using shadowgraphic measurement." Physics of Fluids 9, (1997c): 3111-3113. https://doi.org/10.1063/1.869428
Bau, H H. "Control of Marangoni-Benard convection." International Journal of Heat and Mass Transfer 42, no. 7 (1999): 1327-1341. https://doi.org/10.1016/S0017-9310(98)00234-8
Hashim, I., and Siri, Z. "Stabilization of steady and oscillatory Marangoni instability in rotating fluid layer by feedback control strategy." Numerical Heat Transfer, Part A: Applications 54, no. 6 (2008): 647-663. https://doi.org/10.1080/10407780802289384
Siri, Z., Mustafa, Z., and Hashim, I. "Effects of rotation and feedback control on Benard-Marangoni convection." Journal of Heat and Mass Transfer 52, no. 25 (2009): 5770-5775. https://doi.org/10.1016/j.ijheatmasstransfer.2009.07.025
Khalid, I. K., Mokhtar, N. F. M., and Arifin, N. M. "Rayleigh-Benard convection in micropolar fluid with feedback control effect." World Applied Science Journal 21, (2013): 112-118.