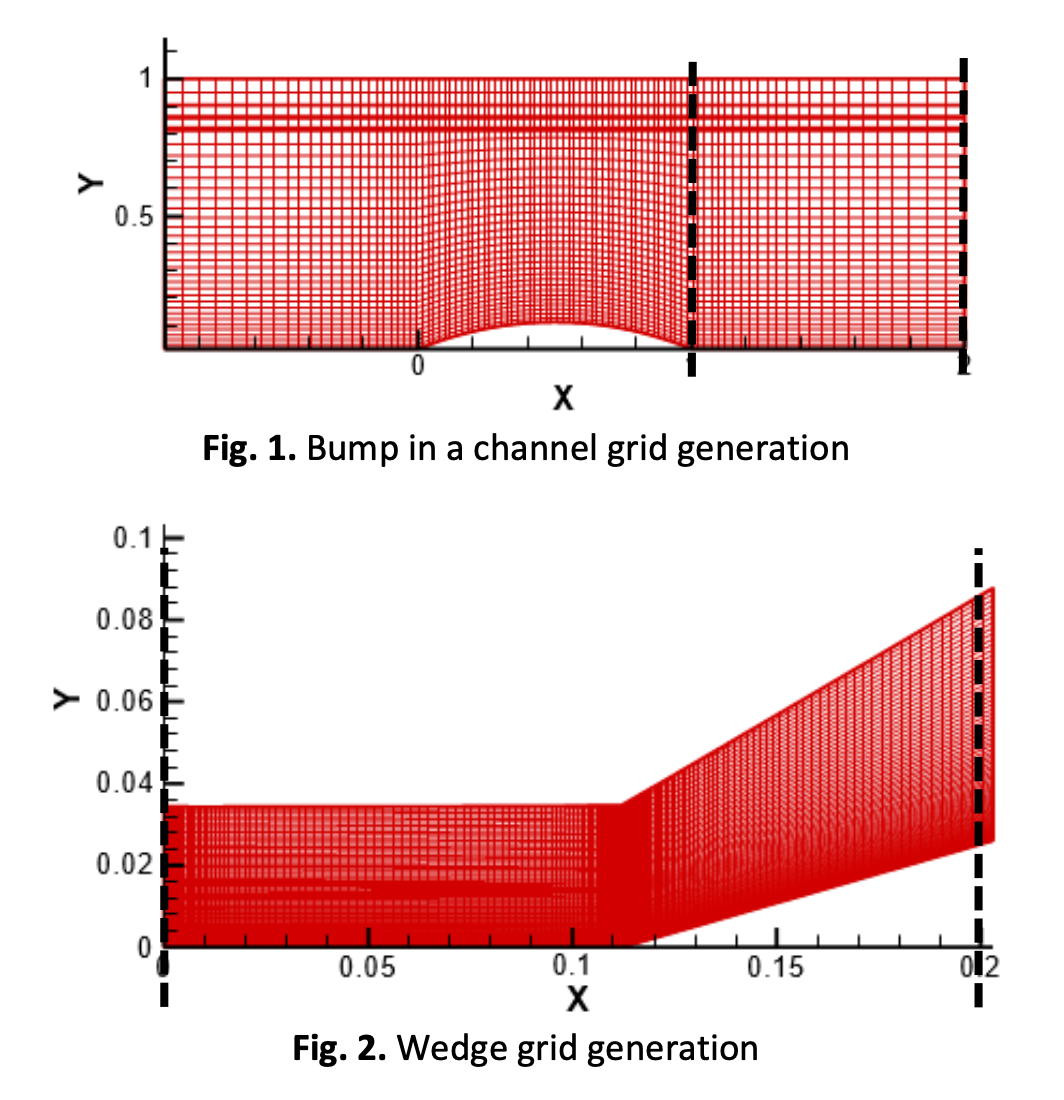
The Influence of Limiters on Davis-Yee and Harten-Yee TVD Schemes
DOI:
https://doi.org/10.37934/cfdl.14.9.1531Keywords:
Euler solver, TVD scheme, shock waveAbstract
TVD schemes have many selections of limiters, but the recommendation of limiters for specific cases is not available in the literature. This study focuses on incorporating two flux limiters as the extension of the TVD schemes proposed by Harten-Yee and Davis-Yee and extends the test case on external flows, blunt-body. The method used in this study is Harten-Yee Upwind TVD and Davis-Yee Symmetric TVD scheme with different limiter functions to simulate cases for two-dimensional compressible flow. The results show that all the limiter functions can capture shock waves when the flow passes through the geometry at Mach number . The flow features such as bow shock, oblique shock, shock wave reflection, interaction, and expansion wave can all be captured in the case of the bump in a channel and wedge. While in the case of the external supersonic flow passing through the blunt-body, the presence of a bow shock was captured. We discovered that Davis-Yee limiter number 2 performs significantly better than other proposed Davis-Yee and Harten-Yee limiters for the case in this study. Therefore, the Davis-Yee Upwind TVD method is recommended to be applied for the identical case on the expansion of this study
Downloads
References
Sa, Luis FN, Carlos M. Okubo, and Emílio C. N. Silva. "Topology optimization of subsonic compressible flows." Structural and Multidisciplinary Optimization 64, no. 1 (2021): 1-22. https://doi.org/10.1007/s00158-021-02903-5
Victoria Rolandi, Laura, Thierry Jardin, Jérôme Fontane, Jérémie Gressier, and Laurent Joly. "Stability of the low Reynolds number compressible flow past a NACA0012 airfoil." AIAA Journal 60, no. 2 (2022): 1052-1066. https://doi.org/10.2514/1.J060792
Constantin, Peter, and Vlad Vicol. "Remarks on high Reynolds numbers hydrodynamics and the inviscid limit." Journal of Nonlinear Science 28, no. 2 (2018): 711-724. https://doi.org/10.1007/s00332-017-9424-z
Ranocha, Hendrik, Lisandro Dalcin, Matteo Parsani, and David I. Ketcheson. "Optimized Runge-Kutta methods with automatic step size control for compressible computational fluid dynamics." Communications on Applied Mathematics and Computation (2021): 1-38. https://doi.org/10.1007/s42967-021-00159-w
Sun, Zheng, and Chi-wang Shu. "Strong stability of explicit Runge--Kutta time discretizations." SIAM Journal on Numerical Analysis 57, no. 3 (2019): 1158-1182. https://doi.org/10.1137/18M122892X
Bhatt, Ashish, and Brian E. Moore. "Structure-preserving Exponential Runge--Kutta Methods." SIAM Journal on Scientific Computing 39, no. 2 (2017): A593-A612. https://doi.org/10.1137/16M1071171
Bai, Feng-peng, Zhong-hua Yang, and Wu-gang Zhou. "Study of total variation diminishing (TVD) slope limiters in dam-break flow simulation." Water Science and Engineering 11, no. 1 (2018): 68-74. https://doi.org/10.1016/j.wse.2017.09.004
Lin, Lei, and Zhe Liu. "TVDal: Total variation diminishing scheme with alternating limiters to balance numerical compression and diffusion." Ocean Modelling 134 (2019): 42-50. https://doi.org/10.1016/j.ocemod.2019.01.002
Saldía, J., S. Elaskar, and J. Tamagno. "Numerical simulations using tvd schemes of two-dimensional supersonic flow in chemical equilibrium." International Journal of Computational Methods 14, no. 2 (2017): 1750020. https://doi.org/10.1142/S0219876217500207
de Goes Maciel, Edisson Savio, and Cláudia Regina de Andrade. "Comparison among unstructured TVD, ENO and UNO schemes in two-and three-dimensions." Applied Mathematics and Computation 321 (2018): 130-175. https://doi.org/10.1016/j.amc.2017.10.026
Hou, Jingming, Qiuhua Liang, Zhanbin Li, Shifeng Wang, and Reinhard Hinkelmann. "Numerical error control for second-order explicit TVD scheme with limiters in advection simulation." Computers & Mathematics with Applications 70, no. 9 (2015): 2197-2209. https://doi.org/10.1016/j.camwa.2015.08.022
Yadegari, Mitra, and M. H. Jahdi. "Capturing of Shock Wave of Supersonic Flow over the Bump Channel with TVD, ACM and Jameson Methods." Iranian Journal of Mechanical Engineering Transactions of the ISME 22, no. 1 (2021): 108-126.
Farzi, Javad, and Fayyaz Khodadosti. "A total variation diminishing high resolution scheme for nonlinear conservation laws." Computational Methods for Differential Equations 6, no. 4 (2018): 456-470.
Yee, Helen C. On the implementation of a class of upwind schemes for system of hyperbolic conservation laws. No. NAS 1.15: 86839. 1985.
Harada, Shigeki, Justin Augustinus, Klaus Hoffmann, Ramesh Agarwal, Shigeki Harada, Justin Augustinus, Klaus Hoffmann, and Ramesh Agarwal. "Development of a modified Runge-Kutta scheme with TVD limiters for the ideal 1-D MHD equations." In 13th Computational Fluid Dynamics Conference, p. 2090. 1997. https://doi.org/10.2514/6.1997-2090
Reddy, Suryakumar, and Michael Papadakis. "TVD schemes and their relation to artificial dissipation." In 31st Aerospace Sciences Meeting, p. 70. 1993. https://doi.org/10.2514/6.1993-70
Hejranfar, Kazem, and Saman Rahmani. "Numerical simulation of shock-disturbances interaction in high-speed compressible inviscid flow over a blunt nose using weighted essentially non-oscillatory scheme." Wave Motion 88 (2019): 167-195. https://doi.org/10.1016/j.wavemoti.2019.03.014
Hixon, R., S-H. Shih, T. Dong, and R. Mankbadi. "Evaluation of generalized curvilinear coordinate transformations applied to high-accuracy finite-difference schemes." In 36th AIAA Aerospace Sciences Meeting and Exhibit, p. 370. 1998. https://doi.org/10.2514/6.1998-370
Demirdžić, I., Ž. Lilek, and M. Perić. "A collocated finite volume method for predicting flows at all speeds." International Journal for Numerical Methods in Fluids 16, no. 12 (1993): 1029-1050. https://doi.org/10.1002/fld.1650161202
Alfarawi, Suliman, Azeldin El-sawi, and Hossin Omar. "Exploring Discontinuous Meshing for CFD Modelling of Counter Flow Heat Exchanger." Journal of Advanced Research in Numerical Heat Transfer 5, no. 1 (2021): 26-34.
Harada, Shigeki, Klaus Hoffmann, and Justin Augustinus. "Development of a modified Runge-Kutta scheme with TVD limiters for the ideal two-dimensional MHD equations." In 36th AIAA Aerospace Sciences Meeting and Exhibit, p. 981. 1998. https://doi.org/10.2514/6.1998-981
Kuzmin, Alexander. "Hysteresis of shock wave locations in divergent bent channels." Computers & Fluids 182 (2019): 52-59. https://doi.org/10.1016/j.compfluid.2019.02.016
Bulat, Pavel, Anzhelika Melnikova, Vladimir Upyrev, and Konstantin Volkov. "Refraction of oblique shock wave on a tangential discontinuity." Fluids 6, no. 9 (2021): 301. https://doi.org/10.3390/fluids6090301
Zhang, Yining, Pengfei Yang, Honghui Teng, Hoi Dick Ng, and Chihyung Wen. "Transition between different initiation structures of wedge-induced oblique detonations." AIAA Journal 56, no. 10 (2018): 4016-4023. https://doi.org/10.2514/1.J056831
Landau, Lev Davidovich, and Evgenii Mikhailovich Lifshitz. Fluid Mechanics: Landau and Lifshitz: Course of Theoretical Physics, Volume 6. Vol. 6. Elsevier, 2013.
Sanders, Brett F., and Scott F. Bradford. "Impact of limiters on accuracy of high-resolution flow and transport models." Journal of Engineering Mechanics 132, no. 1 (2006): 87-98. https://doi.org/10.1061/(ASCE)0733-9399(2006)132:1(87)