Approximate Analytical Solution for Time-Fractional Nonlinear Telegraph Equations with Source Term
DOI:
https://doi.org/10.37934/araset.31.1.132143Keywords:
Adomian Polynomials, Nonlinear Telegraph Equations, Multistep, Source Term, Time-Fractional, Reduced Differential Transform MethodAbstract
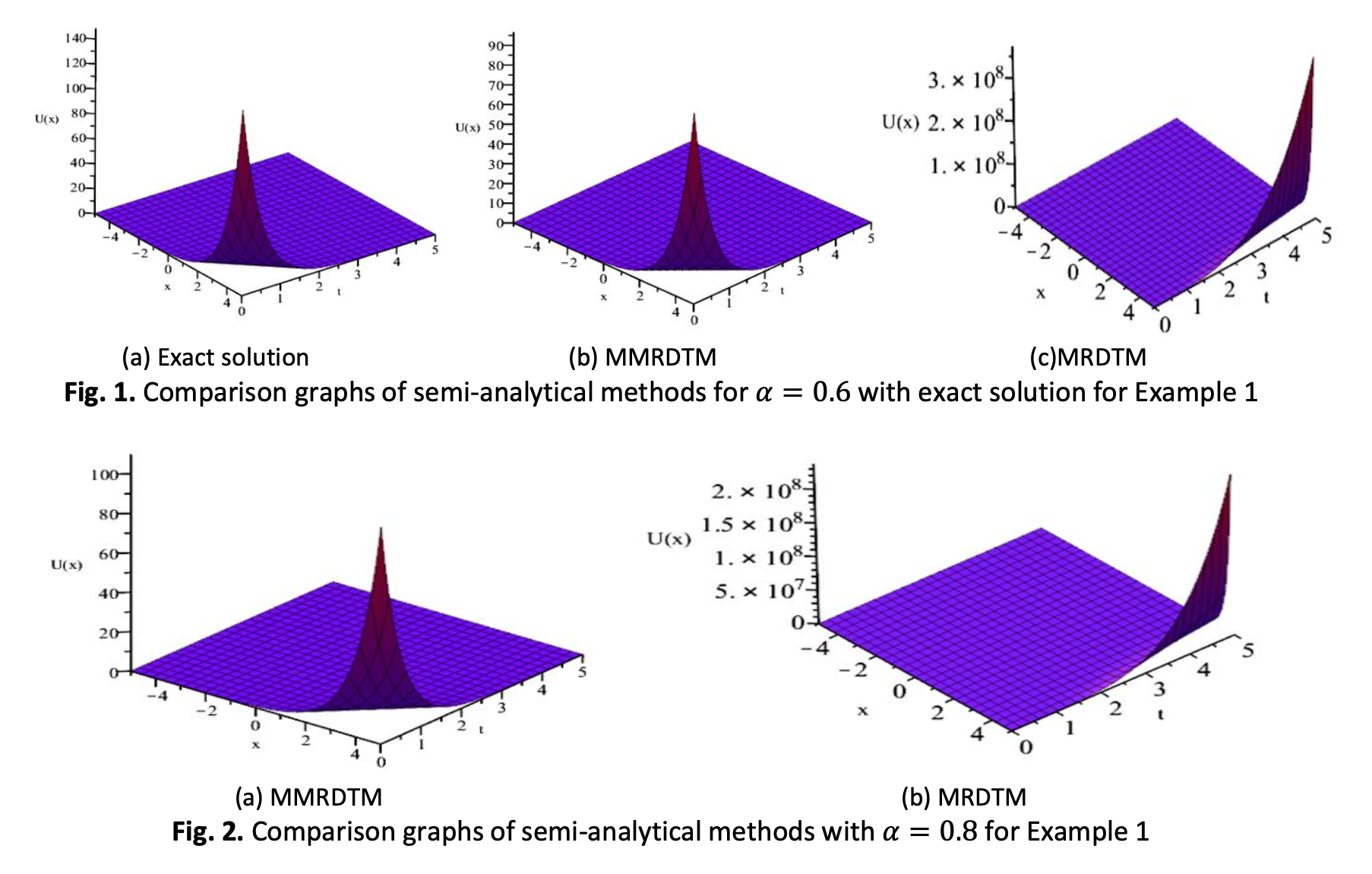
In this study, we considered time-fractional nonlinear telegraph equations (TFNLTEs). For solving the TFNLTEs, we deployed a method known as the Multistep Modified Reduced Differential Transform Method (MMRDTM). Prior to the multistep technique, the nonlinear term in TFNLTEs is replaced with corresponding Adomian polynomials. It can be observed that the MMRDTM is much simpler and more straightforward. On top of that, it works exceptionally where the obtained solutions are more accurately approximated over time. To demonstrate the performance of the MMRDTM in terms of its capabilities and accuracies, we provided two numerical examples of solving TFNLTEs by using MMRDTM and Modified Reduced Differential Transform Method (MRDTM). By comparing the absolute errors of the obtained solutions by both methods, we demonstrated that the solutions provided by the MMRDTM much closer to the exact solutions compared to the corresponding solutions yielded by the MRDTM. This justified that the MMRDTM provides highly accurate and precise solutions for the TFNLTEs.
Downloads