A Study for Solving Pseudo-Parabolic Viscous Diffusion, Telegraph, Poisson and Helmholtz PDE using Legendre-Collocation Method
DOI:
https://doi.org/10.37934/araset.41.1.179190Keywords:
Legendre polynomials, collocation method, telegraph, pseudo-parabolic, Poisson, Helmholtz, partial differential equation, differential matrixAbstract
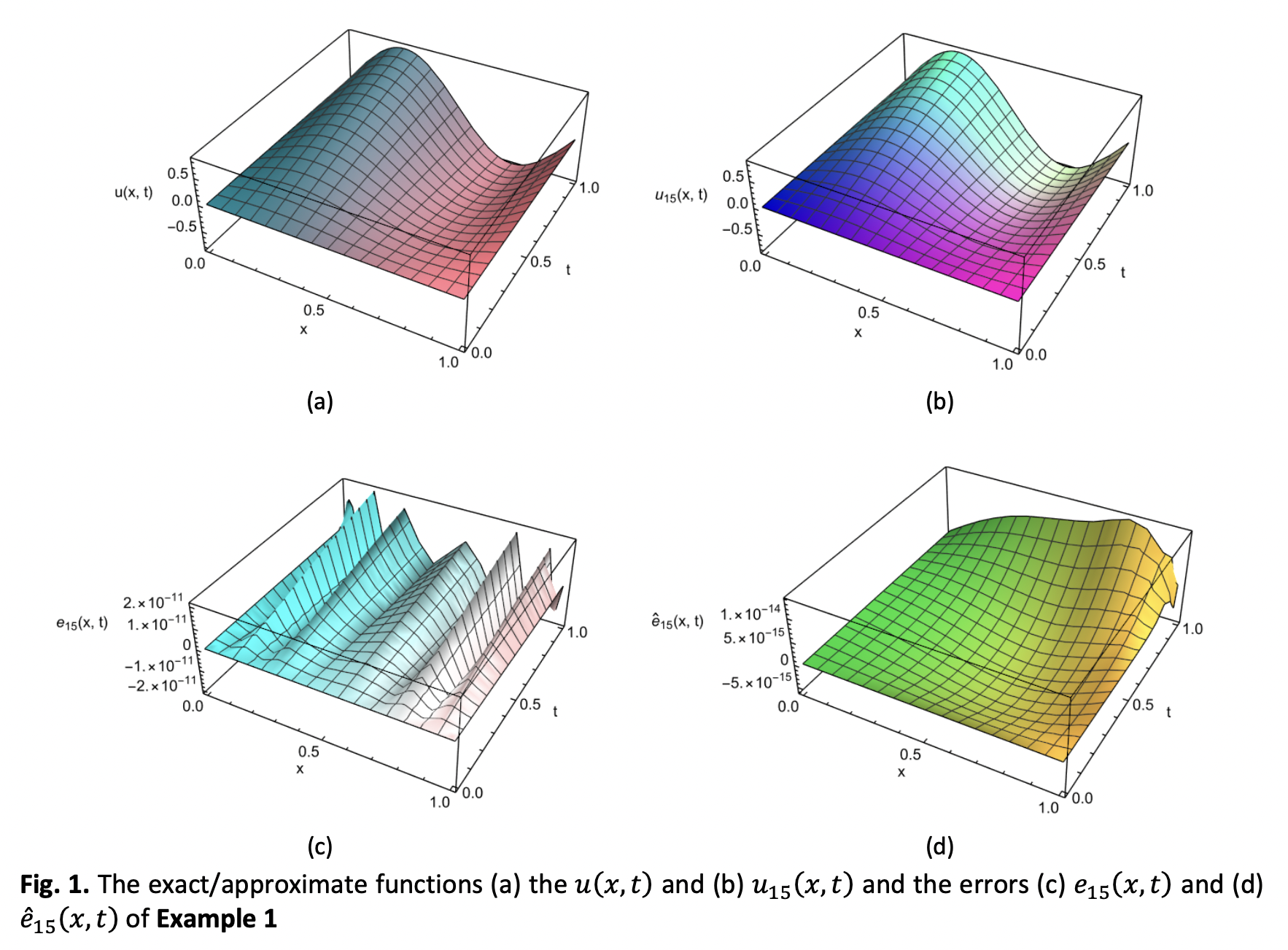
Legendre collocation approach is implemented employing the operative-differential array escorted by the shifted Legendre polynomials. The significance of the proposed approach is reducing the intended partial differential equation problem into an algebraic system of equations by the aid of Legendre polynomials as orthogonal basis. Using mesh collocation points, the domain of the resulting algebraic system solution domain is discretized, and it is then solved to obtain an approximation solution. To demonstrate the accuracy of the procedure, the maximum absolute error and the estimate error are calculated. Also, Illustrative numerical examples are demonstrated to display the veracity of the potential approach in particular pseudo-parabolic viscous diffusion, telegraph, Poisson and Helmholtz partial differential equations. The generated results are contrasted with the exact solutions/other methods to highlight the efficiency of the proposed approach.
Downloads