A Comparative Study on the Performance of Covariance Functions in Gaussian Process Regression Model: Application to Global Wheat Price

Abstract

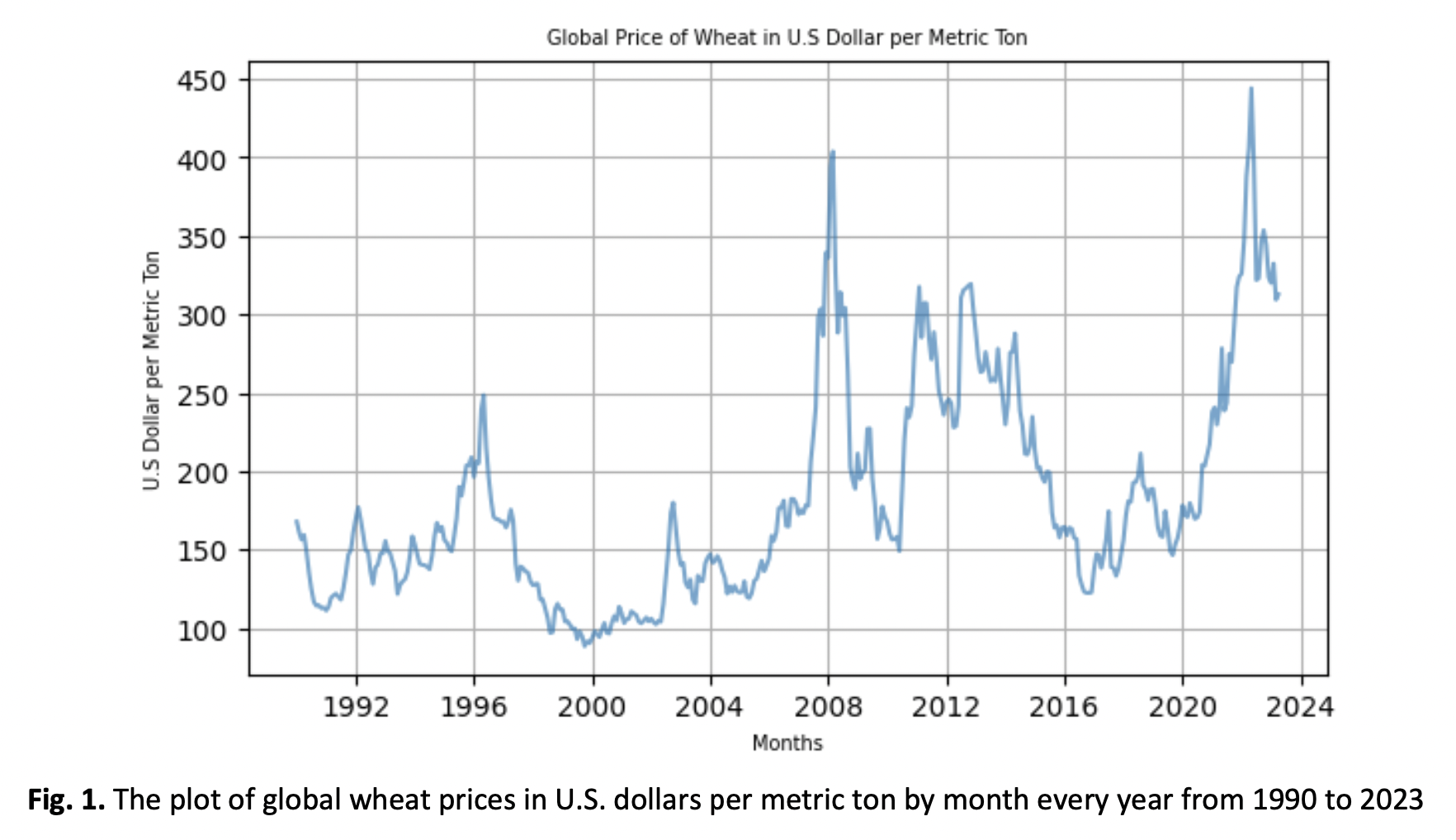
Gaussian Process Regression (GPR) is a nonparametric machine learning model that provides uncertainty quantification in making predictions. GPR utilizes several covariance functions (CFs) in the process of developing models to ensure high accuracy. There are five common CFs in GPR, which are the Radial Basis Function (RBF), Rational Quadratic (RQ), Periodic (Per), Matérn 3/2 (Mat 3/2), and Matérn 5/2 (Mat 5/2), where each covariance function (CF) has different characteristics and behaviors. This paper is to investigate the comparative performances of each CF when applied to the Global Wheat Prices dataset. Error metric measurement like Mean Square Error (MSE) and Root Mean Square Error (RMSE), while Coefficient of Variation (CV) for uncertainty quantification measurement is computed for each CF, and comparisons was made among the CFs to conclude the best CF for this application. The lowest values among them will be the best CF for the data. It should be noted that the CV for each model should be less than 5%, and the CF with the smallest value of CV is considered reliable. The five CFs were fit to the Global Wheat Prices dataset, and it was found that the Mat 3/2 produced the best performances with the lowest values of MSE, RMSE, and CV. Mat 3/2 is the most efficient CF for making predictions since it gives the lowest value of error metric measurement and the lowest value of CV under 5% among the other CFs, making it more reliable for modeling. Overall, the outcome shows that Mat 3/2 is the best CF to be used in developing a GPR model to predict Global Wheat Prices dataset.