Solving Linear Volterra-Fredholm Integro-Differential Equations using Chebyshev-Galerkin with Error Estimation

Mohamed Fathy; W. Abbas

doi:10.37934/araset.40.2.163175

Authors

Mohamed Fathy Basic and Applied Science Department, College of Engineering and Technology, Arab Academy for Science, Technology and Maritime Transport, Cairo, Egypt
W. Abbas Basic and Applied Science Department, College of Engineering and Technology, Arab Academy for Science, Technology and Maritime Transport, Cairo, Egypt

DOI:

https://doi.org/10.37934/araset.40.2.163175

Keywords:

Galerkin, Chebyshev, Numerical, Volterra, Fredholm, Integro-differential equations

Abstract

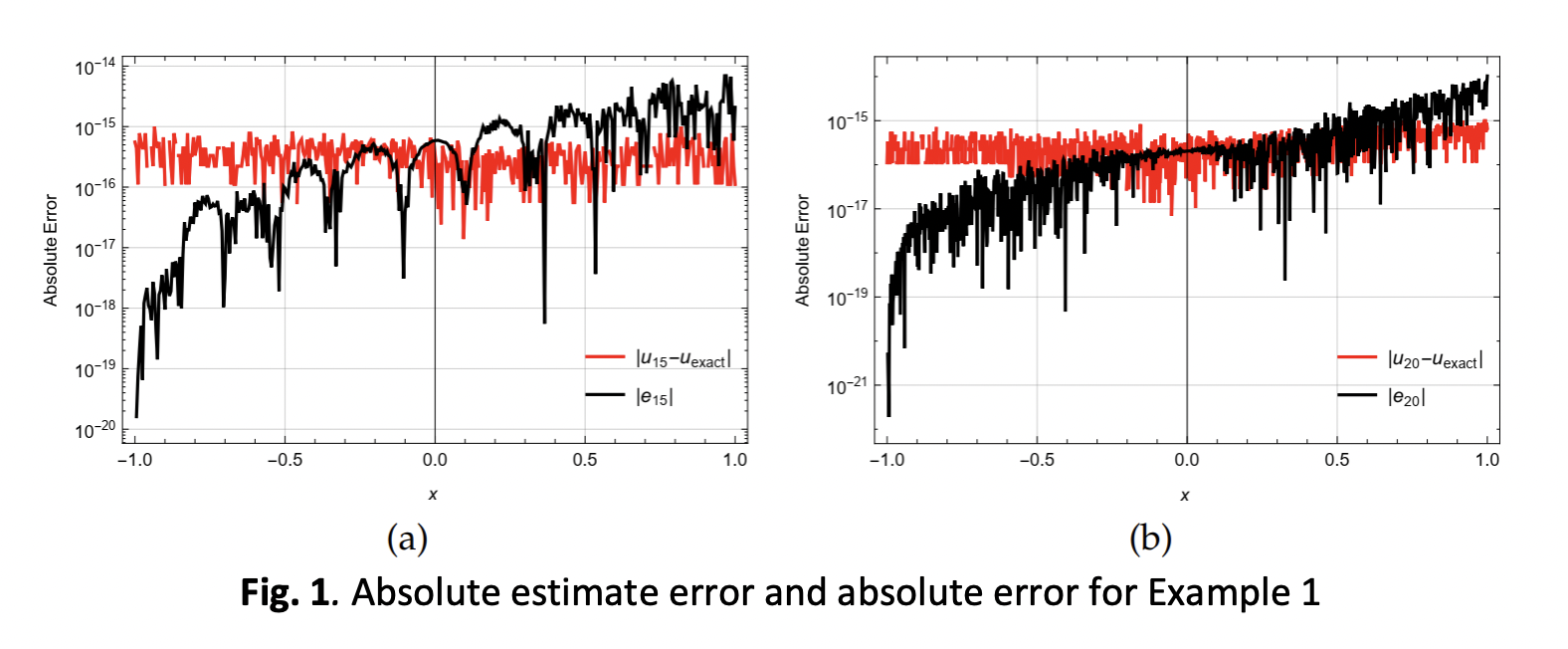
The semi-analytic method based on the Galerkin technique with Chebyshev basis is presented in this paper to solve the linear integro-differential equations in the Volterra-Fredholm type. To facilitate, the use of the Chebyshev-Galerkin technique, new theorems and lemmas are established. Different numerical examples are introduced to demonstrate how the proposed method has efficacy and is easier to apply for this problem type. Some issues’ domains don’t match the Chebyshev’s domain. So, how to adequate the solution domain is presented. The error estimate is computed to prove the method's applicability and accuracy of the proposed method for any problem, especially in the case of the exact solution is not easy to determine.