Peristaltic Transport of Bingham Fluid through Nonuniform Channel with Convective Conditions and Lorentz Forces

Abstract

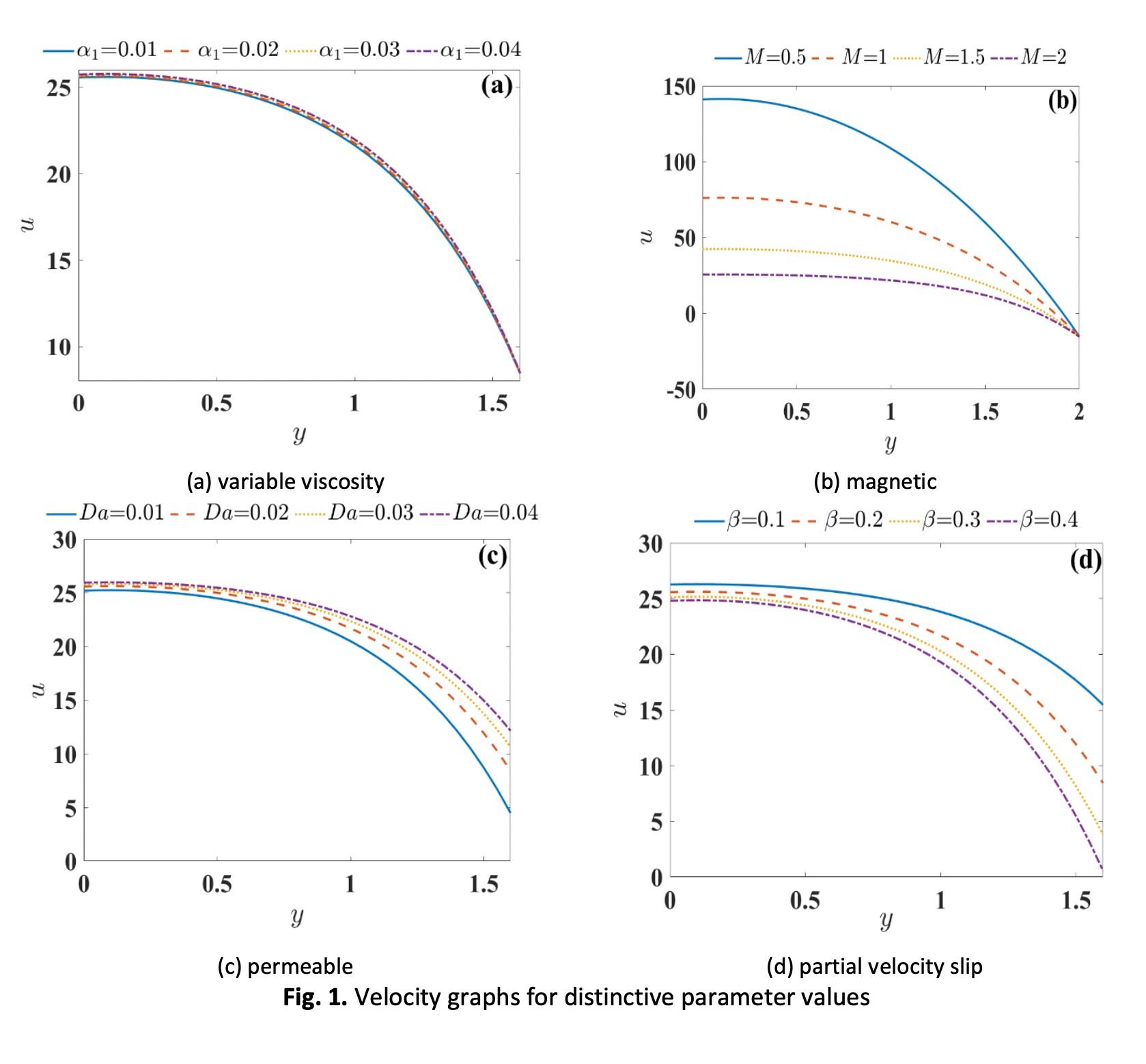
In this study, the impacts of changing the liquid characteristics of the Bingham fluid are highlighted under MHD peristaltic transport. Conditions for convective and porous boundary conditions are taken into consideration. By using proper similarity transformations, the governing equations become dimensionless. For temperature, velocity, and streamlines, the series solution is found. The MATLAB 2019b programming offers a graphical depiction of relevant metrics on physiological flow parameters. The findings demonstrate that lowering the velocity and temperature profiles occurs when the magnetic parameter is increased. Furthermore, the effect of changing viscosity increases the trapped bolus size by a small amount. Once again, the results of the present investigation have significance for our knowledge of the complex rheological mechanisms governing blood flow via small arteries.