Mathematical Modeling on Magnetohydrodynamics Upper Convected Maxwell Fluid Flow Past a Flat Plate Using Spectral Relaxation Approach
DOI:
https://doi.org/10.37934/arfmts.106.1.2338Keywords:
Magnetic field, Maxwell fluid, spectral relaxation approach, thermophysical propertiesAbstract
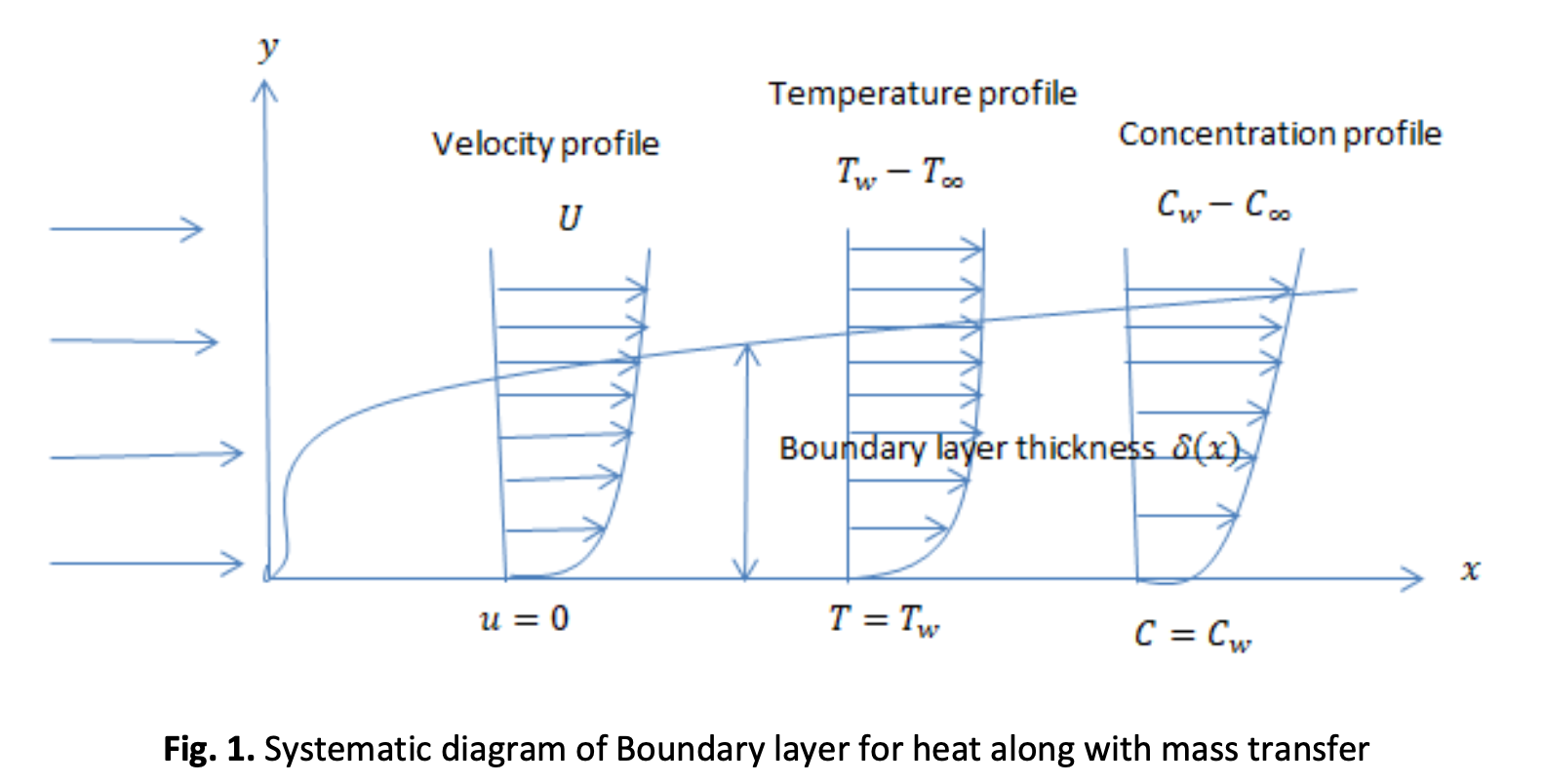
The focus of this treatise is on the scrutiny of MHD heat and mass transfer motion of upper convection Maxwell (UCM) fluid in a thermally radiated flat plate. The models of the flow equations were considered when there is a temperature difference: the Cattaneo-Christov model and the Soret-Dufour mechanisms. A magnetic field of firmness was inflicted in opposition to the flow. The flow inspection is controlled by partial differential equations (PDEs). Suitable similarity variables were utilised on the PDEs to obtain a set of nonlinear ordinary differential equations (ODEs). The simplified set of ODEs shall be answered by exploiting the spectral relaxation method (SRM). The SRM is a numerical technique that solves differential equations by utilising the repetition of a sequence of operations that is iterated iteratively by first decoupling the coupled systems of equations. The magnetism was found to decline the velocity and hydrodynamic boundary layer due to the Lorentz force. The Deborah number was found to enhance the velocity contour. The Eckert number was discovered to improve the temperature profile due to the production of heat energy within the boundary layer. An increase in Prandtl number was found to enhance the hydrodynamic and thermal boundary layer thickness. The local skin friction and Nusselt number were found to be elevated by the increase in the Dufour parameter.
Downloads