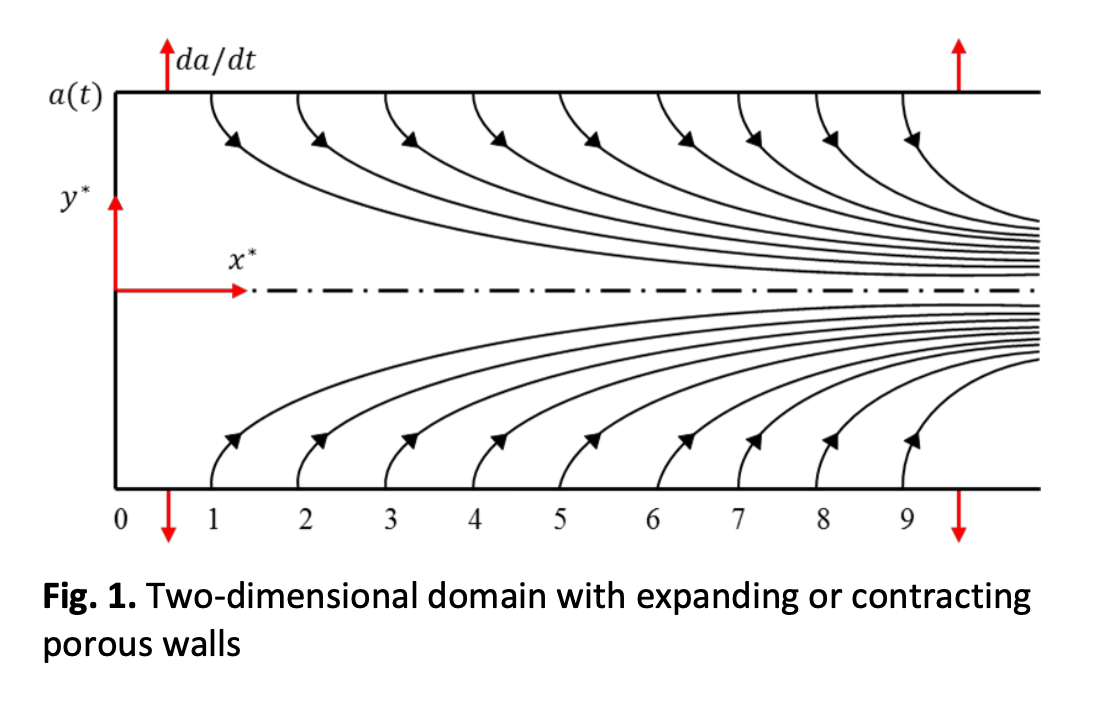
A Well-Founded Analytical Technique to Solve 2D Viscous Flow Between Slowly Expanding or Contracting Walls with Weak Permeability

Yasir Ahmed Abdulameer; Abdul-Sattar Jaber Ali Al-Saif

doi:10.37934/arfmts.97.2.3956

Authors

Yasir Ahmed Abdulameer Department of Mathematics, College of Education for Pure Science, Basrah University, Basrah, Iraq
Abdul-Sattar Jaber Ali Al-Saif Department of Mathematics, College of Education for Pure Science, Basrah University, Basrah, Iraq

DOI:

https://doi.org/10.37934/arfmts.97.2.3956

Keywords:

Fourier transform, homotopy perturbation method, 2D viscous flow, convergence analysis

Abstract

In this article, an analytical technique has been proposed for solving the model of two-dimensional viscous flow between slowly expanding or contracting walls with weak permeability. The idea of combining the Fourier transform and the homotopy perturbation method to yield a new technique was successful. The tables and graphs of the results of new analytical approximate solutions have illustrated the importance, usefulness, and necessity of using the new method. The results obtained showed the accuracy and efficiency of the new method compared to the previous methods, which were used to find the analytical approximate solutions for the current problem.