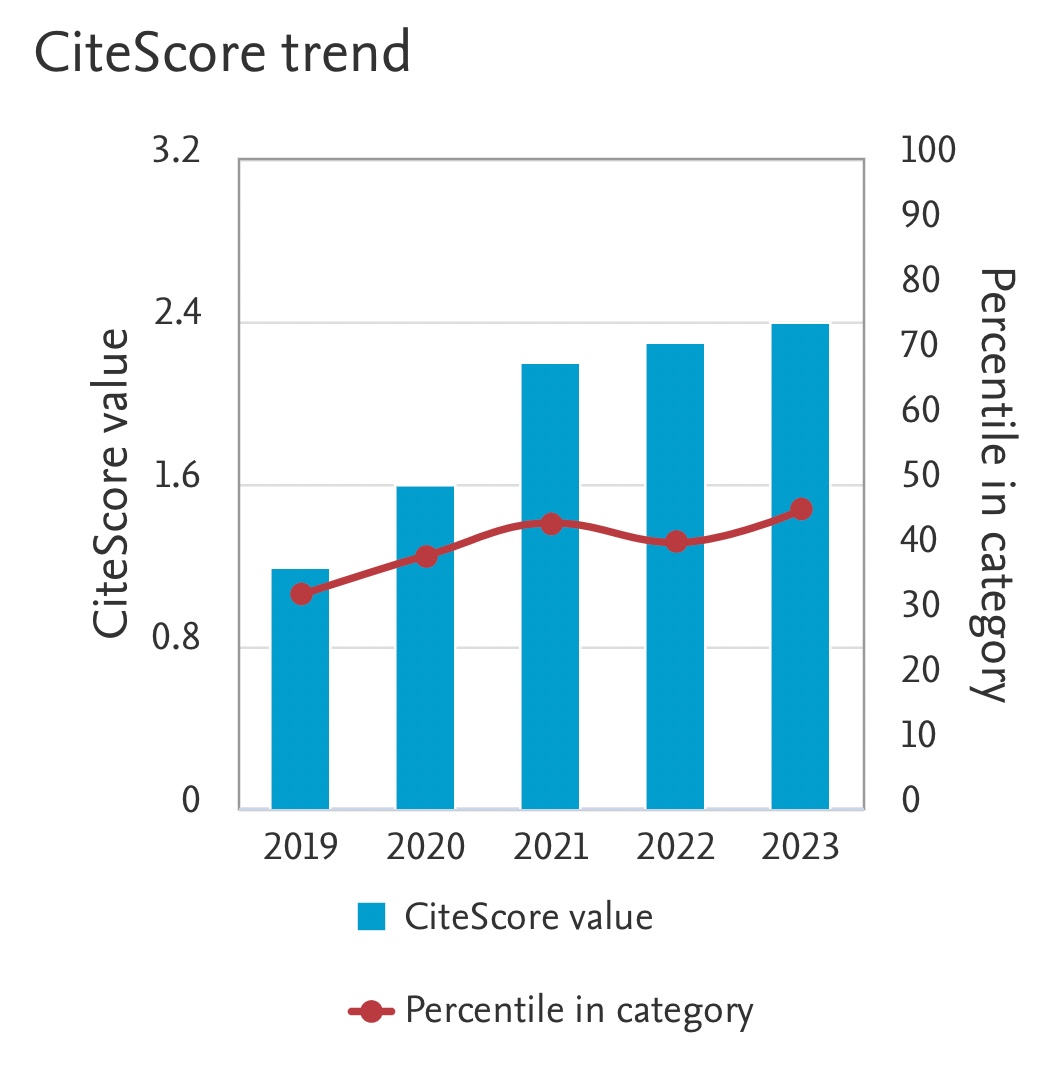
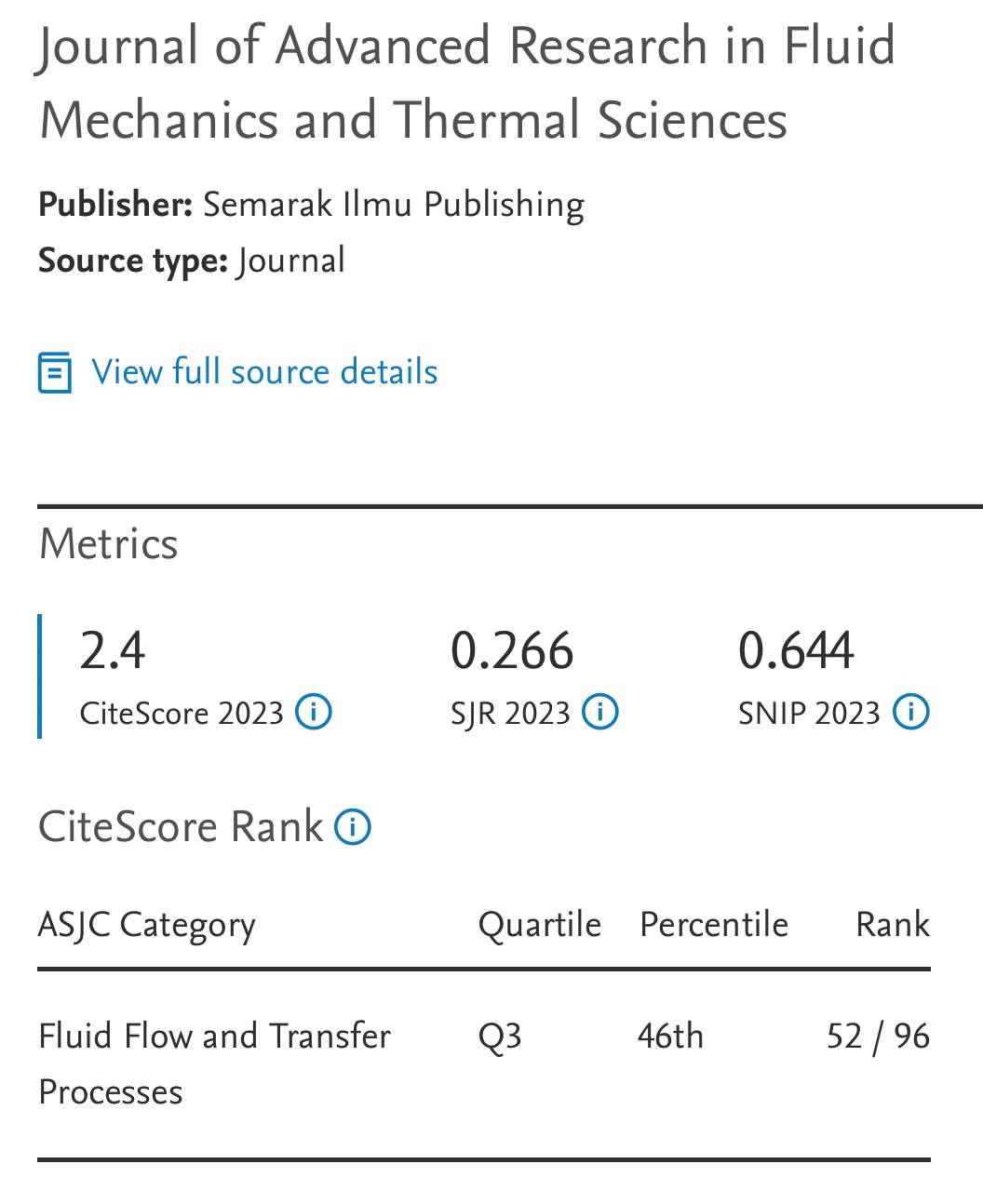
Dean Vortex for Laminar Flows in Curved Pipes with Various Cross-Sections
Keywords:
Dean vortex, Curved pipes;, Various cross-sections, Biharmonic equation, Method of fundamental solutionsAbstract
Curved pipes flows are encountered in different areas such as heat transfer, chaotic mixing, separation of mixtures in pipes, or blood circulation among others and exhibit a variety of characteristics depending on the ranges of Dean numbers and pipe curvatures. Studies on curved pipes flows usually consider the cases of circular, elliptical, and rectangular shapes for the cross sections of the pipe. The present work extends the availability of asymptotic analytical solutions to new ranges of cross-sectional shapes while considering fully developed steady state flows at low Dean numbers. The new shapes are given by a polar equation R* (q) satisfying the relation 1-R^(*2) (q)+dR^(*y) (q)sin(yq)=0 where d and y are parameters. The zero-order azimuthal velocity profiles for various cross-sections are given by exact analytical solutions. Solutions for the nonhomogeneous biharmonic equation for the secondary flows are given by using exact expressions for the particular solutions. Furthermore, the Fourier series decomposition of the solution is adopted to determine the integration constants that allow satisfying the non-slip boundary conditions. Solutions are presented for semi triangular (y=3) , square (y=4), and pentagonal (y=5) cross sections shapes. It is found that the velocity distribution and the Dean’s vortexes intensities are modified in function of the cross-section shapes.
Downloads