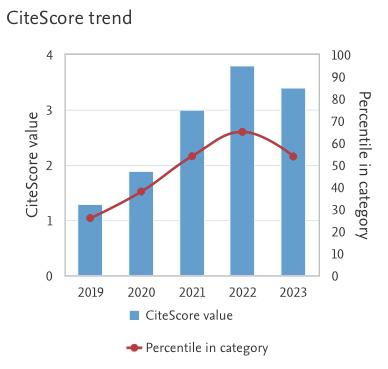
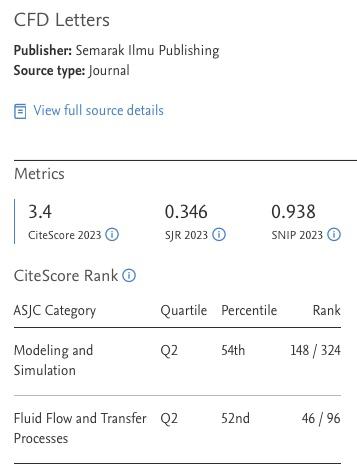
Numerical Computations of Biomagnetic Fluid Flow in a Lid  Driven Cavity

Normazni Abdullah; Zuhaila Ismail; Adrian Syah Halifi; Alia Rafiza Che Ayob; Norsarahaida Saidina Amin; Erwan Hafizi Kasiman

Authors

Normazni Abdullah Department of Mathematical Sciences, Faculty of Science, Universiti Teknologi Malaysia, 81310 Skudai, Johor, Malaysia
Zuhaila Ismail Department of Mathematical Sciences, Faculty of Science, Universiti Teknologi Malaysia, 81310 Skudai, Johor, Malaysia
Adrian Syah Halifi Department of Mathematical Sciences, Faculty of Science, Universiti Teknologi Malaysia, 81310 Skudai, Johor, Malaysia
Alia Rafiza Che Ayob Department of Mathematical Sciences, Faculty of Science, Universiti Teknologi Malaysia, 81310 Skudai, Johor, Malaysia
Norsarahaida Saidina Amin Department of Mathematical Sciences, Faculty of Science, Universiti Teknologi Malaysia, 81310 Skudai, Johor, Malaysia
Erwan Hafizi Kasiman Department of Water and Environmental Engineering, Faculty of Engineering, Universiti Teknologi Malaysia, 81310 Skudai, Johor, Malaysia

Keywords:

Biomagnetic Fluid Dynamics, Finite Element Method, Finite Difference Method

Abstract

The study on the effects of biological fluids in the presence of magnetic field is known as biomagnetic fluid dynamics (BFD) and the most common biological fluid that exhibit such magnetic properties is blood. An extensive research work has been done in this area due to its applications in medical and bioengineering. Basically, it is essential for a study to be justified according to certain benchmark before progressing. Hence, biomagnetic fluid flow in a lid driven cavity is numerically investigated by utilizing two numerical schemes: finite difference and finite element methods. The formulation adopted is consistent with the principles of ferrohydrodynamics. The mathematical model describes Newtonian blood flow under the influence of a spatially varying magnetic field. The model considers the biofluid as non-conducting. The flow is assumed to be two-dimensional, steady, laminar and isothermal. The implementation of finite element method shows stability issue due to extremely steep magnetic field gradient while finite difference method shows no issue. Due to this, a solution is proposed to alleviate the problem and the result for various magnetic field intensity presented.