Numerical Analysis of Blood Flow Behaviour in a Constricted Porous Bifurcated Artery under the Influence of Magnetic Field
DOI:
https://doi.org/10.37934/cfdl.15.1.3958Keywords:
Galerkin least-squares, non-Newtonian, Bifurcated artery, Overlapping stenosis, Magnetohydrodynamics, PorosityAbstract
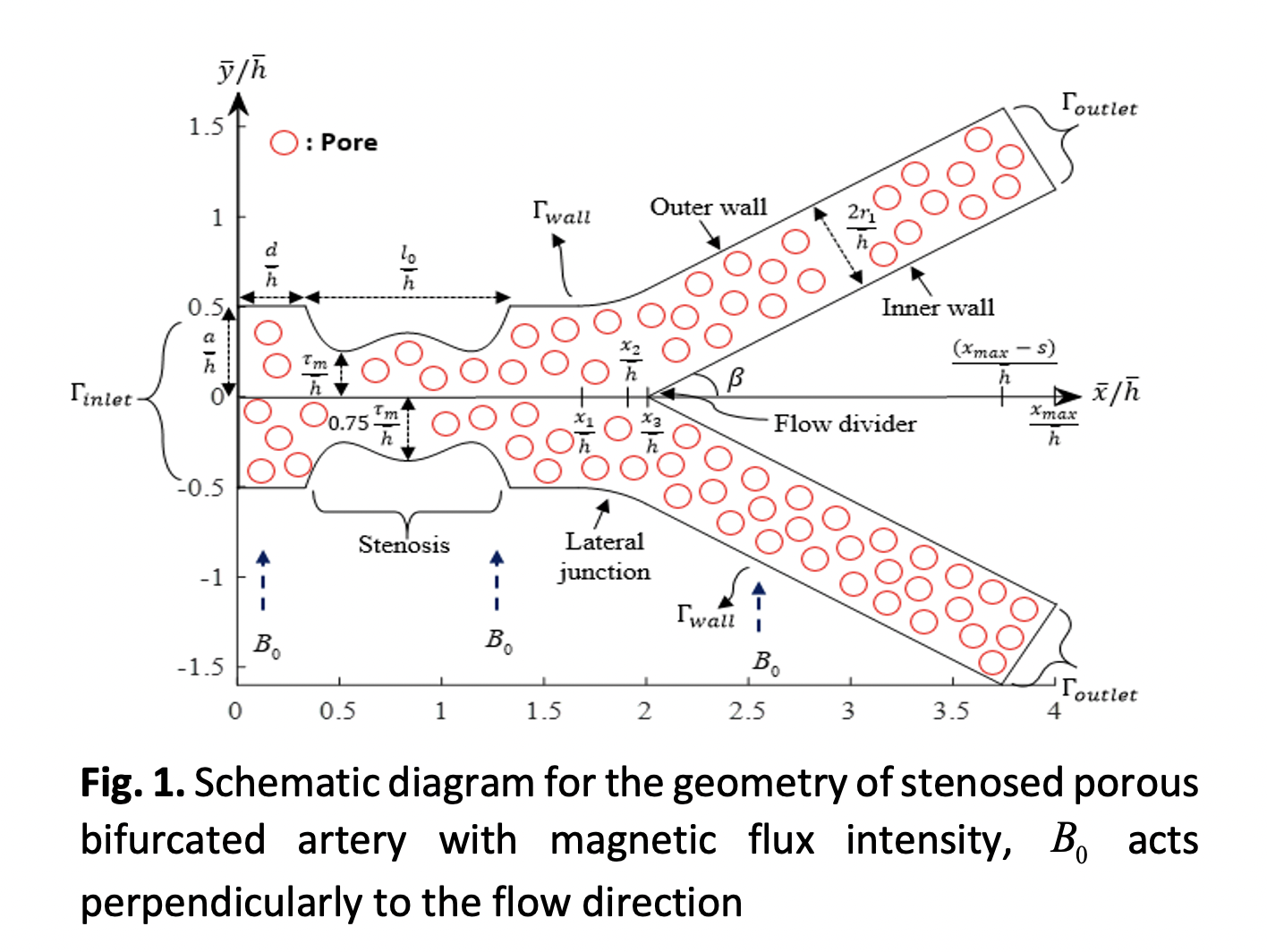
A numerical investigation concerning the effect of arterial constriction on the flow behaviour of blood in a porous bifurcated artery under the influence of a transverse magnetic field has been carried out. The equations of motion governing the flow are derived in the Cartesian coordinate system by treating the fluid as an electrically conducting, Newtonian, incompressible and fully developed blood flow. The blood is considered to flow through a constricted bifurcated artery with overlapping stenosis located at the mother artery. This developed model is consistent with the principles of magnetohydrodynamics. A stabilized form of finite element method, known as the Galerkin least-squares method is employed in solving the governing equation with suitably prescribed boundary conditions. Then, the non-linear systems resulting from the developed model are linearized by an iterative technique called the Newton-Raphson method. The effects of various parameters particularly the severity of stenosis, magnetohydrodynamics constant and permeability parameter on blood flow characteristics are analysed graphically for the velocity profile and streamline pattern. The findings obtained show that the presence of a magnetic field caused a significant alteration in the blood flow behaviour. Slight changes occurred in the flow pattern with the porous medium consideration. The application of a magnetic field could be utilized in controlling the hemodynamic flow of blood by decelerating the flow velocity and reducing the vortex sizes with rising in Hartmann number. While the pathological state of arterial disease as a porous structure reveals that a more porous fluid medium could have slightly promoted the growth in vortex size.Downloads
Download data is not yet available.