Numerical Simulation of Mass Transport Phenomena on Non-newtonian Magnetohydrodynamics Flow of Blood through a Porous Stenosed Bifurcated Artery
DOI:
https://doi.org/10.37934/cfdl.17.1.90113Keywords:
Mass transfer, magnetohydrodynamic, porosity, overlapping stenosis, bifurcated artery, Galerkin least-squaresAbstract
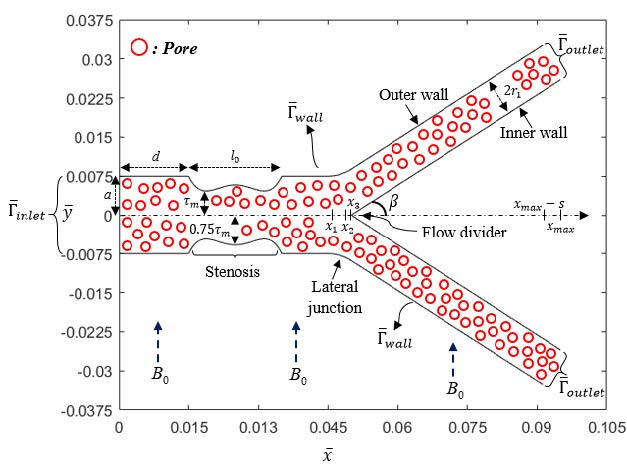
The transport of atherogenic molecules across a bifurcated artery under the stenotic conditions are examined in this present work simultaneously with the effects of magnetohydrodynamics and non-Newtonian flow of blood. The streaming blood is characterised as the power law rheological model that pass through a constricted vessel which acts as a porous medium considering that stenosis is developed from the deposition of fatty substance. This abnormal growth of plaque accumulation which deposited at lumen of the mother artery is modelled as an overlapping shaped stenosis and can be categorized as multiple stenoses. The incompressible, steady, laminar and viscous flow of blood is governed by the continuity, Navier-Stokes and convection-diffusion equations coupled with the non-Newtonian constitutive equation. The equations governing such fluid motion with appropriate boundary conditions are then numerically solved by a stabilized form of finite element approach known as Galerkin least-squares method. The computational domain and dependent variables are both being approximated by quadratic triangular element interpolation function of isoparametric formulation. Effects of different fluids characterisation and magnetic field has been validated and show a satisfactory agreement with findings from previous literatures, thus verify the applicability of the developed algorithms. The findings on the contour filled of velocity with streamlines pattern, contour field of shear stress distribution and contour filled of concentration are simulated with varying hemodynamic parameters of magnetic intensity and porosity constant. The simulated findings have revealed that shear-thinning fluid is vulnerable to an increasing extension of cholesterol accumulation, particularly in the downstream region of stenosis. This vulnerability is predominantly observed when the largest flow separating region and lowest luminal mass transfer coincide, especially when accompanied by the highest flow porosity and magnetic source application, as compared to its counterpart.
Downloads
References
Schade, David S., Deborah Helitzer, and Philip Eaton. "Evidence that low density lipoprotein is the primary cause of atherosclerotic cardiovascular disease: a Bradford-Hill approach." World Journal of Cardiovascular Diseases 7, no. 9 (2017): 271-284.
Liu, Yadong, and Wenjun Liu. "Blood flow analysis in tapered stenosed arteries with the influence of heat and mass transfer." Journal of Applied Mathematics and Computing 63, no. 1 (2020): 523-541. https://doi.org/10.1007/s12190-020-01328-5
Alsemiry, Reima D., Prashanta K. Mandal, Hamed M. Sayed, and Norsarahaida Amin. "Numerical solution of blood flow and mass transport in an elastic tube with multiple stenoses." BioMed research international 2020 (2020). https://doi.org/10.1155/2020/7609562
Sarifuddin, Santabrata Chakravarty, Prashanta Kumar Mandal, and Helge I. Andersson. "Mass transfer to blood flowing through arterial stenosis." Zeitschrift für angewandte Mathematik und Physik 60 (2009): 299-323. https://doi.org/10.1007/s00033-008-7094-2
Mwapinga, Annord, Eunice Mureithi, James Makungu, and Verdiana Masanja. "Non-Newtonian heat and mass transfer on MHD blood flow through a stenosed artery in the presence of body exercise and chemical reaction." Commun. Math. Biol. Neurosci. 2020 (2020): Article-ID.https://doi.org/10.28919/cmbn/4906
Amos, E., E. Omamoke, and Chinedu Nwaigwe. "Chemical reaction, heat source and slip effects on MHD pulsatory blood flowing past an inclined stenosed artery influenced by body acceleration." International Journal of Mathematics Trends and Technology-IJMTT 68 (2022).
Chakravarty, Santabrata, and Subir Sen. "Dynamic response of heat and mass transfer in blood flow through stenosed bifurcated arteries." Korea-Australia Rheology Journal 17, no. 2 (2005): 47-62.
Iasiello, Marcello, Kambiz Vafai, Assunta Andreozzi, and Nicola Bianco. "Analysis of non-Newtonian effects on low-density lipoprotein accumulation in an artery." Journal of biomechanics 49, no. 9 (2016): 1437-1446. doi: 10.1016/j.jbiomech.2016.03.017
Hossain, Khan Enaet, and Md Mohidul Haque. "Influence of magnetic field on chemically reactive blood flow through stenosed bifurcated arteries." In AIP Conference Proceedings, vol. 1851, no. 1. AIP Publishing, 2017.doi: 10.1063/1.4984641
Kumar, Devendra, B. Satyanarayana, Rajesh Kumar, Sanjeev Kumar, and Narendra Deo. "Application of heat source and chemical reaction in MHD blood flow through permeable bifurcated arteries with inclined magnetic field in tumor treatments." Results in Applied Mathematics 10 (2021): 100151. https://doi.org/10.1016/j.rinam.2021.100151
Thirunanasambantham, Kannigah, Zuhaila Ismail, Lim Yeou Jiann, and Amnani Shamjuddin. "Numerical Computational of Blood Flow and Mass Transport in Stenosed Bifurcated Artery." Journal of Advanced Research in Fluid Mechanics and Thermal Sciences 110, no. 2 (2023): 79-94. https://doi.org/10.37934/arfmts.110.2.7994
Khan, Ansab Azam, Khairy Zaimi, Suliadi Firdaus Sufahani, and Mohammad Ferdows. "MHD Flow and Heat Transfer of Double Stratified Micropolar Fluid over a Vertical Permeable Shrinking/Stretching Sheet with Chemical Reaction and Heat Source." Journal of Advanced Research in Applied Sciences and Engineering Technology 21, no. 1 (2020):1-14. https://doi.org/10.37934/araset.21.1.114
Misra, J. C., A. Sinha, and G. C. Shit. "Mathematical modeling of blood flow in a porous vessel having double stenoses in the presence of an external magnetic field." International Journal of Biomathematics 4, no. 02 (2011): 207-225.
Sinha, A., J. C. Misra, and G. C. Shit. "Effect of heat transfer on unsteady MHD flow of blood in a permeable vessel in the presence of non-uniform heat source." Alexandria Engineering Journal 55, no. 3 (2016): 2023-2033. https://doi.org/10.1016/j.aej.2016.07.010
Sankar, A.R., Gunakala, S.R., Comissiong, D.M.G., Gunakala, S.R., and Comissiong, D.M.G. "Two-layered Blood Flow through a Composite Stenosis in the Presence of a Magnetic Field." International Journal of Application or Innovation in Engineering & Management (IJAIEM) 2, no. 12 (2013): 30-41.
Saket, R. K., and Anil Kumar. "Reliability of Convective Diffusion Process in Stenosis Blood Vessels." Chemical product and process modeling 3, no. 1 (2008). https://doi.org/10.2202/1934-2659.1175
Nandal, J., S. Kumari, and R. Rathee. "The effect of slip velocity on unsteady peristalsis MHD blood flow through a constricted artery experiencing body acceleration." International Journal of Applied Mechanics and Engineering 24, no. 3 (2019): 645-659. https://doi.org/10.2478/ijame-2019-0040
Nadeem, S., Noreen Sher Akbar, T. Hayat, and Awatif A. Hendi. "Influence of heat and mass transfer on Newtonian biomagnetic fluid of blood flow through a tapered porous arteries with a stenosis." Transport in porous media 91 (2012): 81-100. https://doi.org/10.1007/s11242-011-9834-6
Omar, Nur Fatihah Mod, Husna Izzati Osman, Ahmad Qushairi Mohamad, Rahimah Jusoh, and Zulkhibri Ismail. "Analytical solution of unsteady MHD casson fluid with thermal radiation and chemical reaction in porous medium." Journal of Advanced Research in Applied Sciences and Engineering Technology 29, no. 2 (2023): 185-194. https://doi.org/10.37934/araset.29.2.185194
Omamoke, Ekakitie, and Emeka, Amos. "Chemical Reaction, Radiation and Heat Source Effects on Unsteady MHD Blood Flow Over a Horizontal Porous Surface in the Presence of an Inclined Magnetic Field." International Journal of Scientific & Engineering Research 11, no. 4 (2020): 1187-1192.
Abdullahi, Isah, A. A. Hussaini, Domven Lohcwat, Ali Musa, and Mohammed Adamu. "Influence of Chemical Reaction, Heat Source and Thermal radiation on MHD Blood flow through a Porous Medium with an Inclined Magnetic field in Treatments of Cardiovascular Diseases." GSJ 10, no. 3 (2022).
Chakravarty, Santabrata, and Prashanta Kumar Mandal. "An analysis of pulsatile flow in a model aortic bifurcation." International journal of engineering science 35, no. 4 (1997): 409-422. https://doi.org/10.1016/S0020-7225(96)00081-X
Chakravarty, S., and P. K. Mandal. "Mathematical modelling of blood flow through an overlapping arterial stenosis." Mathematical and computer modelling 19, no. 1 (1994): 59-70.https://doi.org/10.1016/0895-7177(94)90116-3
Husain, Iqbal, Fotini Labropulu, Chris Langdon, and Justin Schwark. "A comparison of Newtonian and non-Newtonian models for pulsatile blood flow simulations." Journal of the Mechanical Behaviour of Materials 21, no. 5-6 (2013): 147-153. https://doi.org/10.1515/jmbm-2013-0001
Sousa, Luisa, C. A. T. A. R. I. N. A. Castro, C. A. R. L. O. S. Antonio, and R. Chaves. "Computational techniques and validation of blood flow simulation." WEAS Transactions on biology and biomedicine, ISI/SCI Web of Science and Web of Knowledge 8, no. 04 (2011): 145-155.
Halifi, Adrian S., Sharidan Shafie, and Norsarahaida S. Amin. "Numerical solution of biomagnetic power-law fluid flow and heat transfer in a channel." Symmetry 12, no. 12 (2020): 1959. https://doi.org/10.3390/sym12121959
Zinani, Flávia, and Sérgio Frey. "Galerkin least-squares solutions for purely viscous flows of shear-thinning fluids and regularized yield stress fluids." Journal of the Brazilian Society of Mechanical Sciences and Engineering 29 (2007): 432-443. https://doi.org/10.1590/S1678-58782007000400012
Machado, Fernando, Flávia Zinani, and Sérgio Frey. "Herschel-Bulkley Fluid Flows Through a Sudden Axisymmetric Expansion via Galerkin Least-Squares Methodology." (2007).
Franca, Leopoldo P., and Alexandre L. Madureira. "Element diameter free stability parameters for stabilized methods applied to fluids." Computer methods in applied mechanics and engineering 105, no. 3 (1993): 395-403. https://doi.org/10.1016/0045-7825(93)90065-6
Harari, Isaac, and Thomas JR Hughes. "What are C and h?: Inequalities for the analysis and design of finite element methods." Computer methods in applied mechanics and engineering 97, no. 2 (1992): 157-192. https://doi.org/10.1016/0045-7825(92)90162-D
Bell, Brent C., and Karan S. Surana. "p‐version least squares finite element formulation for two‐dimensional, incompressible, non‐Newtonian isothermal and non‐isothermal fluid flow." International journal for numerical methods in fluids 18, no. 2 (1994): 127-162. https://doi.org/10.1002/fld.1650180202
Ghia, U. K. N. G., Kirti N. Ghia, and C. T. Shin. "High-Re solutions for incompressible flow using the Navier-Stokes equations and a multigrid method." Journal of computational physics 48, no. 3 (1982): 387-411. https://doi.org/10.1016/0021-9991(82)90058-4
Papafaklis, Michail I., and Lampros K. Michalis. "Intravascular Imaging and Haemodynamics: The Role of Shear Stress in Atherosclerosis and In-Stent Restenosis." In Intravascular Imaging: Current Applications and Research Developments, pp. 326-348. IGI Global, 2012. https://doi.org/10.4018/978-1-61350-095-8.ch019
Abdelwahab, A. M., Kh S. Mekheimer, Khalid K. Ali, A. El-Kholy, and N. S. Sweed. "Numerical simulation of electroosmotic force on micropolar pulsatile bloodstream through aneurysm and stenosis of carotid." Waves in Random and Complex Media (2021): 1-32. https://doi.org/10.1080/17455030.2021.1989517
Weddell, Jared C., JaeHyuk Kwack, P. I. Imoukhuede, and Arif Masud. "Hemodynamic analysis in an idealized artery tree: differences in wall shear stress between Newtonian and non-Newtonian blood models." PloS one 10, no. 4 (2015): e0124575. https://doi.org/10.1371/journal.pone.0124575
Song, Jianfei, Smaine Kouidri, and Farid Bakir. "Numerical study of hemodynamic and diagnostic parameters affected by stenosis in bifurcated artery." Computer Methods in Biomechanics and Biomedical Engineering 23, no. 12 (2020): 894-905.
Arzani, Amirhossein. "Coronary artery plaque growth: A two‐way coupled shear stress–driven model." International journal for numerical methods in biomedical engineering 36, no. 1 (2020): e3293.