Fractional Casson Fluid Flow via Oscillating Motion of Plate and Microchannel
DOI:
https://doi.org/10.37934/cfdl.14.11.18Keywords:
Oscillating motion, fractional derivative, plate, microchannelAbstract
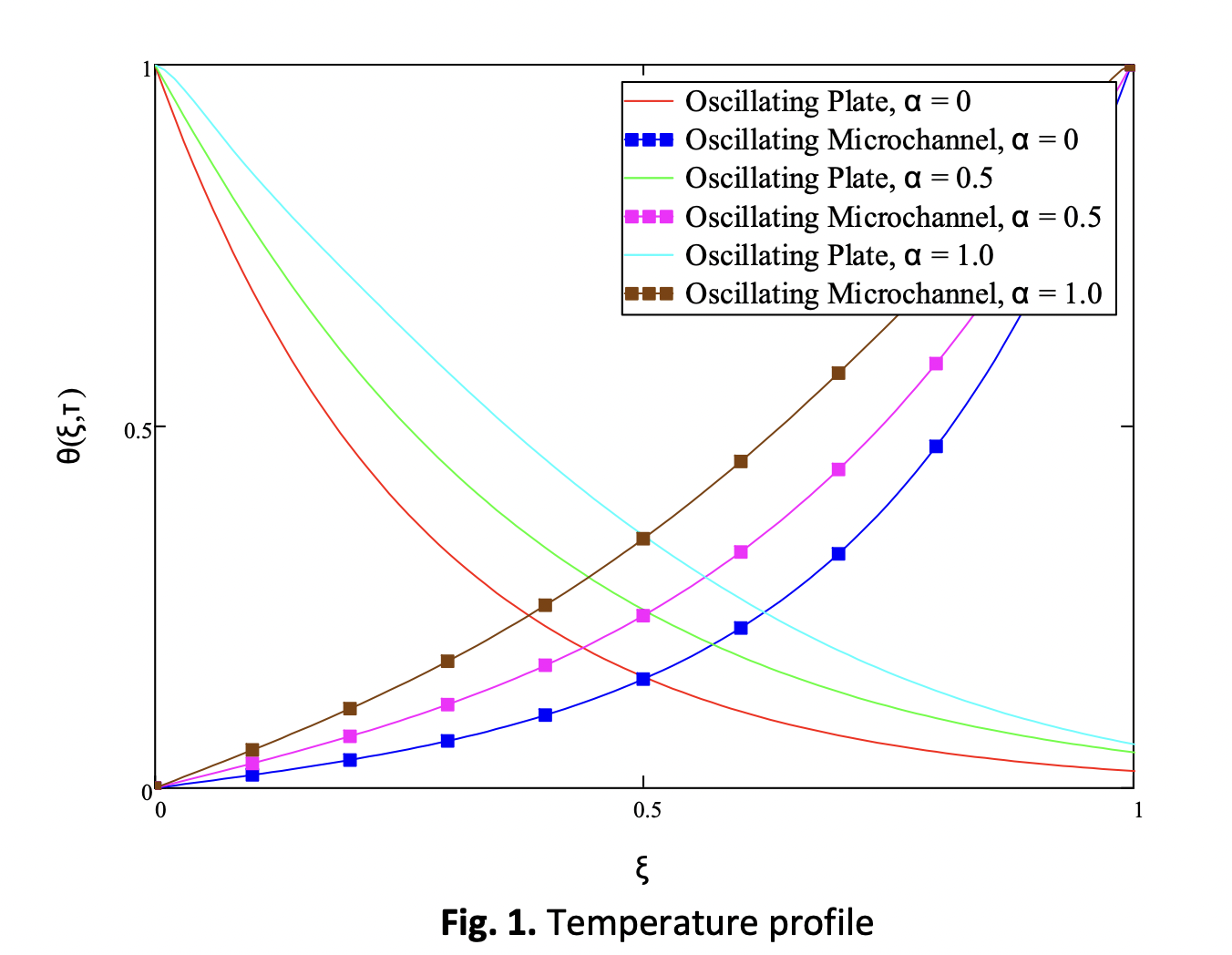
The impact of the Caputo fractional derivative on the unsteady mixed convention boundary layer flow of Casson fluid is investigated. It is evaluated the flow via two different geometries which are plate and microchannel with oscillating motion. The problems are modelled using a set of partial differential equations with appropriate initial and boundary conditions. The dimensional equations are turned into dimensionless governing equations by using relevant dimensionless variables. The obtained solutions are transformed into fractional form using Caputo fractional derivative. The exact solutions are obtained using the Laplace transform approach. Inverse Laplace transform is applied to the oscillating plate problem while Zakian’s explicit formula approach is used to obtain the results of temperature and velocity profiles. Both profiles are graphed and studied its behaviour in both geometries. The temperature profile is shown to have an opposite pattern of graph for both geometries. While when compared between both geometries on its velocity profile, oscillating plate has a higher velocity compared to oscillating plate. For both profiles, increasing the fractional parameter resulted in a greater pattern. This study aids in the comprehension of Casson fluid flows in fractional systems.Downloads
References
Jan, Syed Aftab Alam, Farhad Ali, Nadeem Ahmad Sheikh, Ilyas Khan, Muhammad Saqib, and Madeha Gohar. "Engine oil based generalized brinkman‐type nano‐liquid with molybdenum disulphide nanoparticles of spherical shape: Atangana‐Baleanu fractional model." Numerical Methods for Partial Differential Equations 34, no. 5 (2018): 1472-1488. https://doi.org/10.1002/num.22200
Qureshi, Sania. "Real life application of Caputo fractional derivative for measles epidemiological autonomous dynamical system." Chaos, Solitons & Fractals 134 (2020): 109744. https://doi.org/10.1016/j.chaos.2020.109744
Saqib, Muhammad, Ilyas Khan, and Sharidan Shafie. "New direction of Atangana–Baleanu fractional derivative with Mittag-Leffler kernel for non-Newtonian channel flow." In Fractional Derivatives with Mittag-Leffler Kernel, pp. 253-268. Springer, Cham, 2019. https://doi.org/10.1007/978-3-030-11662-0_15
Abro, Kashif Ali. "Role of fractal–fractional derivative on ferromagnetic fluid via fractal Laplace transform: A first problem via fractal–fractional differential operator." European Journal of Mechanics-B/Fluids 85 (2021): 76-81. https://doi.org/10.1016/j.euromechflu.2020.09.002
Imran, M. A., I. Khan, M. Ahmad, N. A. Shah, and M. Nazar. "Heat and mass transport of differential type fluid with non-integer order time-fractional Caputo derivatives." Journal of Molecular Liquids 229 (2017): 67-75. https://doi.org/10.1016/j.molliq.2016.11.095
Abro, Kashif Ali, and Abdon Atangana. "A comparative study of convective fluid motion in rotating cavity via Atangana–Baleanu and Caputo–Fabrizio fractal–fractional differentiations." The European Physical Journal Plus 135, no. 2 (2020): 1-16. https://doi.org/10.1140/epjp/s13360-020-00136-x
Anwar, Talha, Poom Kumam, and Phatiphat Thounthong. "Fractional Modeling and Exact Solutions to Analyze Thermal Performance of Fe 3 O 4-MoS 2-Water Hybrid Nanofluid Flow Over an Inclined Surface With Ramped Heating and Ramped Boundary Motion." IEEE Access 9 (2021): 12389-12404. https://doi.org/10.1109/ACCESS.2021.3051740
Haque, Ehsan Ul, Aziz Ullah Awan, Nauman Raza, Muhammad Abdullah, and Maqbool Ahmad Chaudhry. "A computational approach for the unsteady flow of Maxwell fluid with Caputo fractional derivatives." Alexandria engineering journal 57, no. 4 (2018): 2601-2608. https://doi.org/10.1016/j.aej.2017.07.012
Abidin, Nurul Hafizah Zainal, Nor Fadzillah Mohd Mokhtar, Izzati Khalidah Khalid, and Siti Nur Aisyah Azeman. "Oscillatory Mode of Darcy-Rayleigh Convection in a Viscoelastic Double Diffusive Binary Fluid Layer Saturated Anisotropic Porous Layer." Journal of Advanced Research in Numerical Heat Transfer 10, no. 1 (2022): 8-19.
Casson, N. "A flow equation for the pigment oil suspension of the printing ink type." Rheology of Disperse Systems: 84-102.
Pramanik, S. "Casson fluid flow and heat transfer past an exponentially porous stretching surface in presence of thermal radiation." Ain Shams Engineering Journal 5, no. 1 (2014): 205-212. https://doi.org/10.1016/j.asej.2013.05.003
Reyaz, Ridhwan, Yeou Jiann Lim, Ahmad Qushairi Mohamad, Muhammad Saqib, and Sharidan Shafie. "Caputo fractional MHD Casson fluid flow over an oscillating plate with thermal radiation." Journal of Advanced Research in Fluid Mechanics and Thermal Sciences 85, no. 2 (2021): 145-158. https://doi.org/10.37934/arfmts.85.2.145158
Sheikh, Nadeem Ahmad, Dennis Ling Chuan Ching, Ilyas Khan, Devendra Kumar, and Kottakkaran Sooppy Nisar. "A new model of fractional Casson fluid based on generalized Fick’s and Fourier’s laws together with heat and mass transfer." Alexandria Engineering Journal 59, no. 5 (2020): 2865-2876. https://doi.org/10.1016/j.aej.2019.12.023
Naqvi, Syed Muhammad Raza Shah, Taseer Muhammad, and Mir Asma. "Hydromagnetic flow of Casson nanofluid over a porous stretching cylinder with Newtonian heat and mass conditions." Physica A: Statistical Mechanics and its Applications 550 (2020): 123988. https://doi.org/10.1016/j.physa.2019.123988
Halsted, D. J., and D. E. Brown. "Zakian's technique for inverting Laplace transforms." The Chemical Engineering Journal 3 (1972): 312-313. https://doi.org/10.1016/0300-9467(72)85037-8
Gudekote, Manjunatha, and Rajashekhar Choudhari. "Slip effects on peristaltic transport of Casson fluid in an inclined elastic tube with porous walls." Journal of Advanced Research in Fluid Mechanics and Thermal Sciences 43, no. 1 (2018): 67-80.
Hamrelaine, Salim, Fateh Mebarek-Oudina, and Mohamed Rafik Sari. "Analysis of MHD Jeffery Hamel flow with suction/injection by homotopy analysis method." Journal of Advanced Research in Fluid Mechanics and Thermal Sciences 58, no. 2 (2019): 173-186.
Wang, Quanrong, and Hongbin Zhan. "On different numerical inverse Laplace methods for solute transport problems." Advances in Water Resources 75 (2015): 80-92. https://doi.org/10.1016/j.advwatres.2014.11.001