Analytical Solutions for Fractional Caputo-Fabrizio Casson Nanofluid on Riga Plate with Newtonian Heating

Abstract

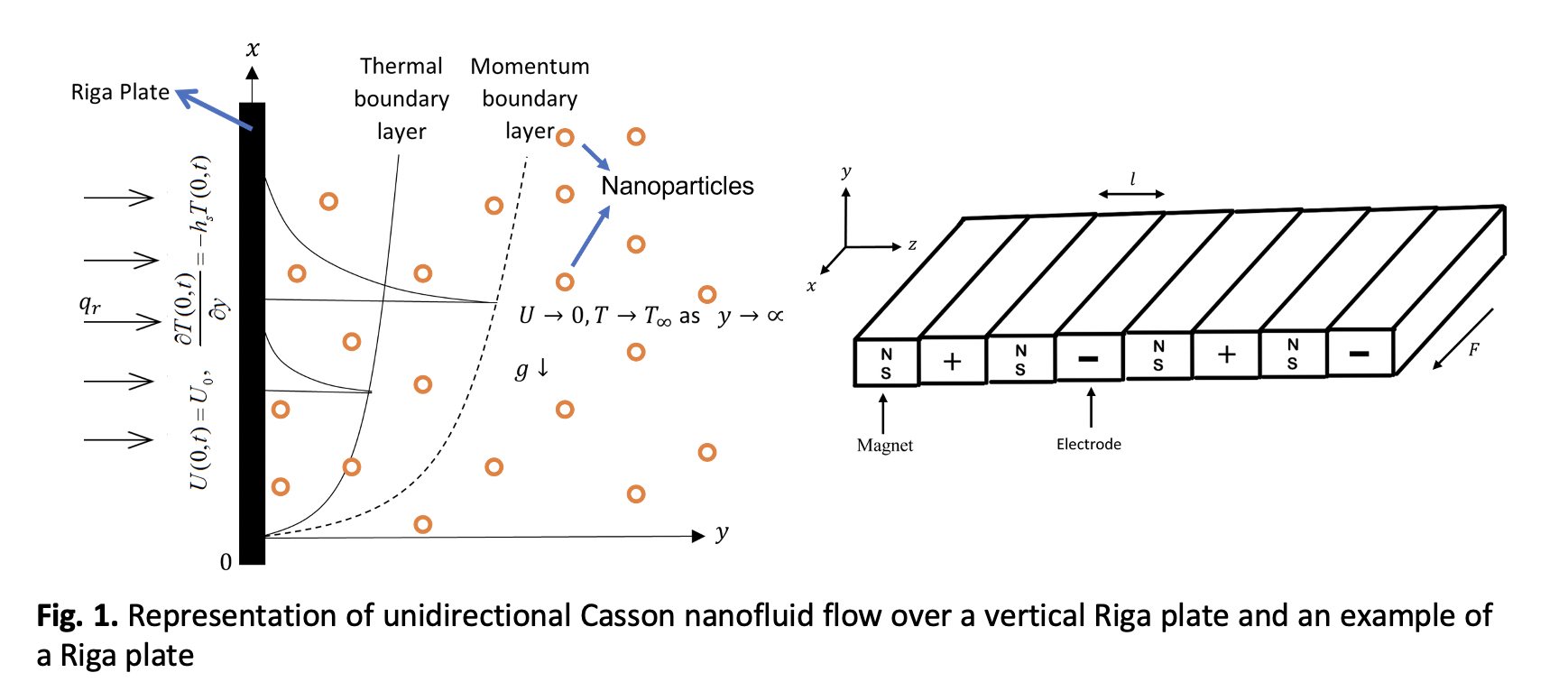
Introduction of fractional derivatives to the mechanics of fluid flow is relatively new. Even though the exact geometrical representations of fractional derivatives on fluid mechanics have not been discovered, recent literatures have proven that it is a paradox that will be useful in the future. Meanwhile, Riga plates are actuators that is convenient for controlling the velocity of fluid flows. Widely used in the field of marine engineering, the properties of fluid flowing over Riga plates are worth investigating. Thus, the aim of this study is to investigate the analytical solutions of an unsteady incompressible Casson nanofluid flowing over a Riga plate with presence of Newtonian heating. Carboxymethyl Cellulose (CMC) water was used as a prime example of Casson fluid with Copper-Oxide (CuO) nanoparticles. Coupled with a non-Newtonian fluid, the Casson fluid, and the Caputo-Fabrizio fractional derivative, the analytical solutions obtained will be beneficial in the engineering world as a tool for validating experimental and numerical studies. Through this study, analytical solutions were obtained and the profiles of both velocity and temperature of fluid with variations in parameters were investigated. It is observed that variations in the fractional derivative parameter produces a spectrum of solutions that abides the initial and boundary conditions set. An amplification of the modified Hartmann number increases both the velocity and temperature profiles, while an amplification of the nanoparticle volume fraction decreases the velocity profile but increase the temperature profile.