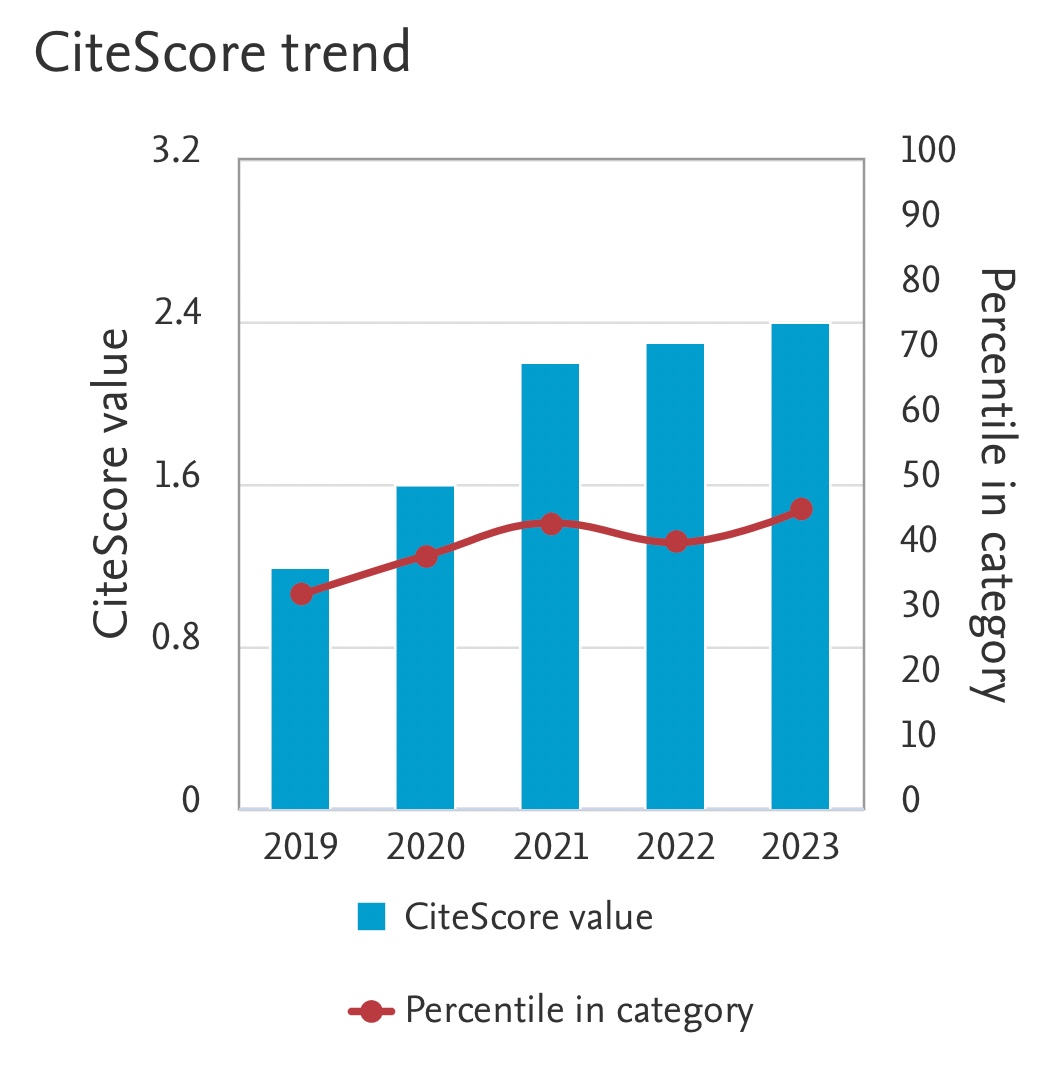
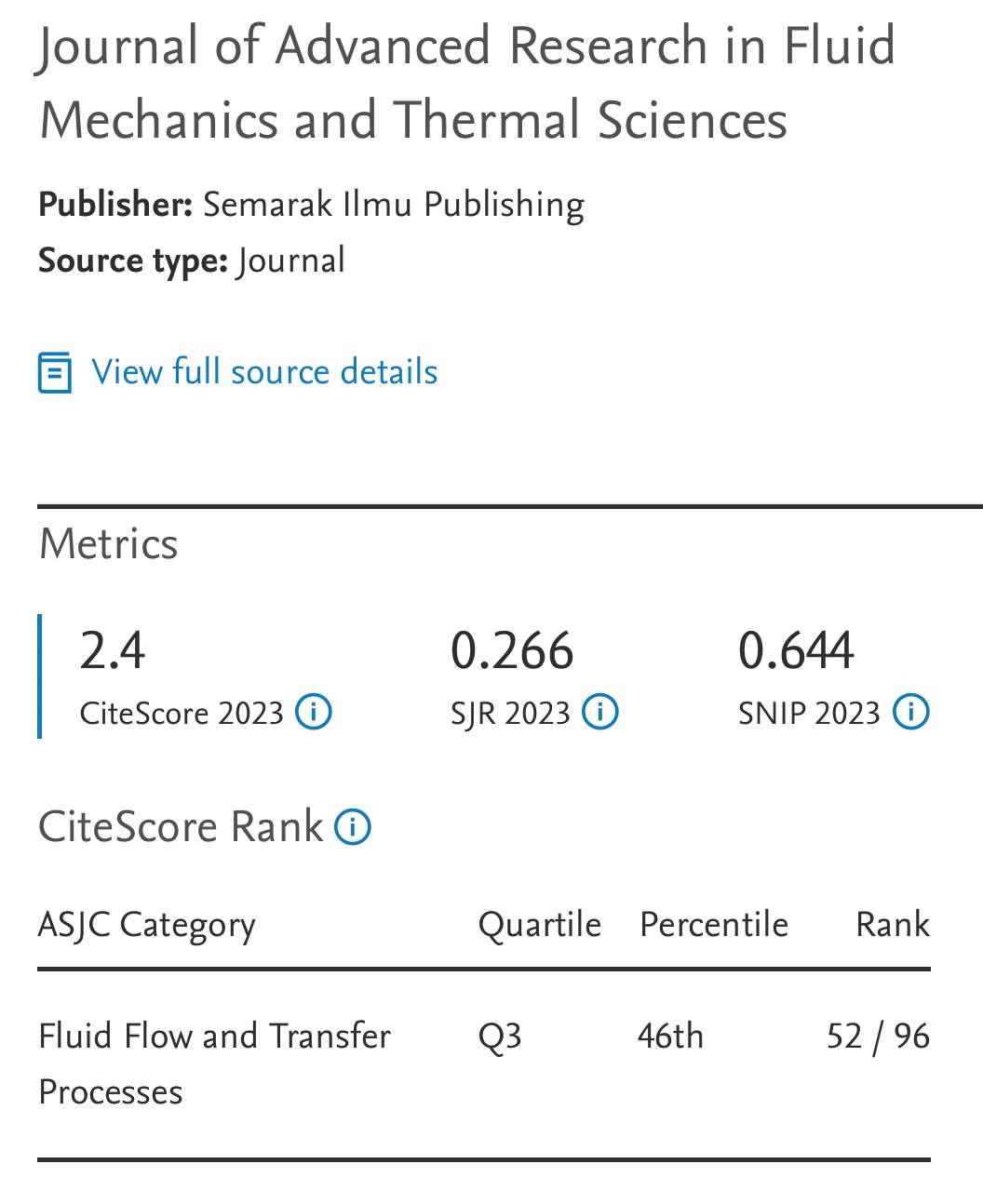
Relationship between Viscosity and Surface Tension as a Solution to Fractional Differential Equations

Abstract

Viscosity, also known as thickness, is the measure of a fluid's resistance to the stress it experiences, caused by cohesive forces between fluid particles. Surface tension is the force or downward pull caused by unbalanced attractive forces at the liquid interface, leading to the contraction of the liquid surface. Numerous studies have been conducted, particularly on determining the relationship between these two phenomena. However, very few studies are associated with fractional differential equations. This paper presents research results based on empirical data obtained from laboratory testing on viscosity and surface tension and explores their interrelationship. Through scatter plot data and regression of logarithmic functions, the obtained function is claimed as a solution to a first-order linear differential equation, with the graph of its solution matching the actual data. Subsequently, this differential equation will be generalized into a fractional differential equation with guaranteed existence and uniqueness of solutions. The method used to find solutions is the Adomian-Laplace Decomposition, and the result is that the graph of the solution function coincides with the graph of the exact solution. This indicates that the relationship between viscosity and surface tension can be described using a solution derived from a fractional differential equation model.