Numerical Investigation on the Conical Flow of Viscoelastic Fluids

AHMED SHAREEF; Alaa Al-Muslimawi

doi:10.37934/cfdl.16.4.8597

Authors

Ahmed M. Shareef Department of Mathematics, College of Science, University of Basrah, Basrah, Iraq
Alaa Al-Muslimawi Department of Mathematics, College of Science, University of Basrah, Basrah, Iraq

DOI:

https://doi.org/10.37934/cfdl.16.4.8597

Keywords:

Galerkin method, Hybrid finite element/volume scheme, Phan–Thien/Tanner model, Stick-slip, Viscoelasticity

Abstract

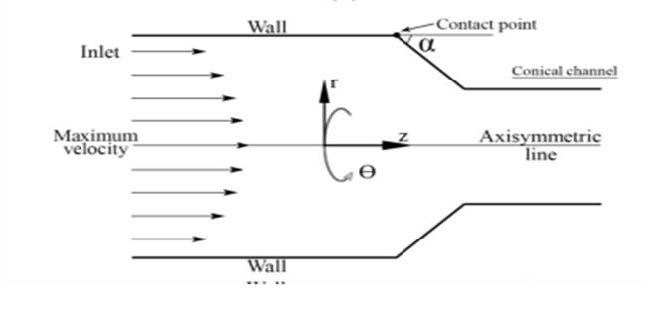
The conical problem represents one of the important problems in the various fields of industrial as the automotive industry and the aerospace industry, due to their great role in controlling the flow of liquids and gases. This article covers a computational investigation of incompressible the Phan–Thien/Tanner shear-thinning viscoelastic fluid flow through a conical converging channel. Here, we select hybrid finite element/finite volume algorithm as a first time to treat such problem. This method consists of the combination of a Taylor-Galerkin/pressure correction finite element method (TGPC-FEM) and a cell-vertex finite volume approach (CV-FEA) to solve the system of partial differential equations that govern the fluid flow. The TGPC-FEM is employed to the momentum and mass conservation models, while the stress constitutive models are treated by finite volume implementation. The findings of current study are concerned with stress response, deformation rate, and pressure drop under variations in Weissenberg number and EPTT parameters. The effect of shear-thinning behaviour with the EPTT representation is also considered.

Downloads

Download data is not yet available.

Author Biographies

Ahmed M. Shareef, Department of Mathematics, College of Science, University of Basrah, Basrah, Iraq

ahmad.muhamad.sci@uobasrah.edu.iq

Alaa Al-Muslimawi , Department of Mathematics, College of Science, University of Basrah, Basrah, Iraq

alaa.abdullah@uobasrah.edu.iq

References

Harrison, W. J. "The pressure in a viscous liquid moving through a channel with diverging boundaries." In Proc Cambridge Phil Soc, vol. 19, pp. 307-312. 1919.

Bond, W. N. "CXIV. Viscous flow through wide-angled cones." The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 50, no. 299 (1925): 1058-1066. https://doi.org/10.1080/14786442508628550

Oka, Syoten, and Akira Takami. "The steady slow motion of a non-Newtonian liquid through a tapered tube." Japanese Journal of Applied Physics 6, no. 4 (1967): 423.

Forsyth, T. H. "Converging flow of polymers." Polymer-Plastics Technology and Engineering 6, no. 1 (1976): 101-131. https://doi.org/10.1080/03602557608055823

Sutterby, John L. "Laminar converging flow of dilute polymer solutions in conical sections. II." Transactions of the Society of Rheology 9, no. 2 (1965): 227-241. https://doi.org/10.1122/1.549024

Kwon, T. H., S. F. Shen, and K. K. Wang. "Pressure drop of polymeric melts in conical converging flow: Experiments and predictions." Polymer Engineering & Science 26, no. 3 (1986): 214-224. https://doi.org/10.1002/pen.760260306

Kajiwara, T., S. Ninomiya, Y. Kuwano, and K. Funatsu. "Numerical simulation of converging flow of polymer melts through a tapered slit die." Journal of non-newtonian fluid mechanics 48, no. 1-2 (1993): 111-124. https://doi.org/10.1016/0377-0257(93)80067-L

Jarzebski, A. B., and W. L. Wilkinson. "Non-isothermal developing flow of a generalised power-law fluid in a tapered tube." Journal of Non-Newtonian Fluid Mechanics 8, no. 3-4 (1981): 239-248. https://doi.org/10.1016/0377-0257(81)80023-7

Settles, Gary S., and Hsueh-Ying Teng. "Cylindrical and conical flow regimes of three-dimensional shock/boundary-layer interactions." AIAA journal 22, no. 2 (1984): 194-200. https://doi.org/10.2514/3.8367

Sutterby, J. L. "Laminar converging flow of dilute polymer solutions in conical sections: Part I. Viscosity data, new viscosity model, tube flow solution." AIChE Journal 12, no. 1 (1966): 63-68. https://doi.org/10.1002/aic.690120114

Abdulhasan, Ahmed N., and Alaa H. Al-Muslimawi. "Numerical investigation of extensional flow through axisymmetric conical geometries: Finite element method." Basrah Journal of Science 38, no. 3 (2020): 399-421.

Cogswell, F. N. "Converging flow and stretching flow: a compilation." Journal of Non-Newtonian Fluid Mechanics 4, no. 1-2 (1978): 23-38. https://doi.org/10.1016/0377-0257(78)85004-6

Al-Muslimawi, A., H. R. Tamaddon-Jahromi, and M. F. Webster. "Simulation of viscoelastic and viscoelastoplastic die-swell flows." Journal of Non-Newtonian Fluid Mechanics 191 (2013): 45-56. https://doi.org/10.1016/j.jnnfm.2012.08.004

Wapperom, P., and M. F. Webster. "A second-order hybrid finite-element/volume method for viscoelastic flows." Journal of Non-Newtonian Fluid Mechanics 79, no. 2-3 (1998): 405-431. https://doi.org/10.1016/S0377-0257(98)00124-4

Aboubacar, M., H. Matallah, and M. F. Webster. "Highly elastic solutions for Oldroyd-B and Phan-Thien/Tanner fluids with a finite volume/element method: planar contraction flows." Journal of Non-Newtonian Fluid Mechanics 103, no. 1 (2002): 65-103. https://doi.org/10.1016/S0377-0257(01)00164-1

Al-Muslimawi, A., H. R. Tamaddon-Jahromi, and M. F. Webster. "Numerical simulation of tube-tooling cable-coating with polymer melts." Korea-Australia Rheology Journal 25 (2013): 197-216. . https://doi.org/10.1007/s13367-013-0021-x

Al-Muslimawi, Alaa H. "Numerical study for differential constitutive equations with polymer melts by using a hybrid finite-element/volume method." Journal of Computational and Applied Mathematics 308 (2016): 488-498. https://doi.org/10.1016/j.cam.2016.06.007

Townsend, P., and M. F. Webster. "An algorithm for the three-dimensional transient simulation of non-Newtonian fluid flows." In Proc. Int. Conf. Num. Meth. Eng.: Theory and Applications, NUMETA, Nijhoff, Dordrecht, vol. 12, pp. 1-11. 1987.

Matallah, H., P. Townsend, and M. F. Webster. "Recovery and stress-splitting schemes for viscoelastic flows." Journal of Non-Newtonian Fluid Mechanics 75, no. 2-3 (1998): 139-166. https://doi.org/10.1016/S0377-0257(97)00085-2

Hasan, Zinah Abdulkadhim, and Abdul-Sattar J. Al-Saif. "A new approach to solving two-dimensional unsteady incompressible Navier-Stokes equations." Journal of Applied Mathematics and Physics 10, no. 10 (2022): 3218-3239.

Aboubacar, M., H. Matallah, H. R. Tamaddon-Jahromi, and M. F. Webster. "Numerical prediction of extensional flows in contraction geometries: hybrid finite volume/element method." Journal of non-newtonian fluid mechanics 104, no. 2-3 (2002): 125-164. https://doi.org/10.1016/S0377-0257(02)00015-0

Yasir, Reisan Y., Alaa H. Al-Muslimawi, and Bashaeer K. Jassim. "Numerical simulation of non-Newtonian inelastic flows in channel based on artificial compressibility method." Journal of Applied and Computational Mechanics 6, no. 2 (2020): 271-283.

Al-Muslimawi, Alaa H. "Taylor Galerkin pressure correction (TGPC) finite element method for incompressible Newtonian cable-coating flows." Journal of Kufa for Mathematics and Computer 5, no. 2 (2018): 14-22. https://doi.org/10.31642/jokmc/2018/050203

Al-Haboobi, Anas, and Alaa H. Al-Muslimawi. "Novel algorithm for compressible Newtonian axisymmetric thermal flow." International Journal of Modern Physics C 2450025 (2024): 17. https://doi.org/10.1142/S0129183124500256

Sharhan, Alaa, and Alaa H. Al-Muslimawi. "Numerical Study of Shear and Extensional Inelastic Contraction Flows." CFD Letters 15, no. 8 (2023): 107-121. https://doi.org/10.37934/cfdl.15.8.107121

Fadhel, Ihssan A., and Alaa H. Al-Muslimawi. "Numerical simulation of stick-slip viscoelastic fluid by using a hybrid finite-element/volume method." In AIP Conference Proceedings, vol. 2398, no. 1. AIP Publishing, 2022. https://doi.org/10.1063/5.0093620

Fadhel, Ihssan Aqeel, and Alaa Hassan Al-Muslimawi. "Simulation of Oldroyd-B Viscoelastic Fluid in Axisymmetric Straight Channel by Using a Hybrid Finite Element/Volume Method." Journal of Advanced Research in Fluid Mechanics and Thermal Sciences 81, no. 1 (2021): 26-40.