Application of the Grid Convergency Index Method and Courant Number Analysis for Propeller Turbine Simulation

Abstract

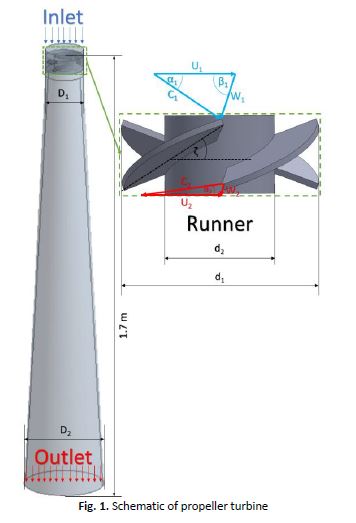
The computational method has long been used in propeller turbine studies. However, there has not yet been a comprehensive explanation for mesh and timestep independency method or verification for propeller turbine simulation. Hence, this study explains propeller turbines' mesh and timestep independency method. The computational software for this case is ANSYS® FLUENT 18.2™. The grid convergency index (GCI) and the Courant number (C_n) analysis determine the optimum mesh and timestep size. Based on the results, the mesh number of 691996 (medium) is considered appropriate in this case because the GCI is below 1%. The 691996 mesh has a size (Δx) of 0.432 mm. The C_n is 0.72 (the water velocity of 0.63 m/s) based on the investigation; therefore, the timestep size for this case of 0.0005s. Then, verification of the CFD results in the propeller turbine can be indicated by visualising the pressure contour; the pressure on the upper side of the runner should be higher than the lower side. The deviation average of CFD results in secondary data of 14.48%. The deviation is presumably because of missed information about the CFD setup geometry with real conditions. Thus, the independency method using the GCI method and C_n analysis is recommended for propeller turbines. CFD results show that torque, power generated, and efficiency of the propeller turbine toward its rotation have a similar pattern to secondary data; it can indicate that the CFD results of the propeller turbine are verified.