The Effect of Different Scale on Object to the Approximation of the First Order Polarization Tensor of Sphere, Ellipsoid, and Cube

Abstract

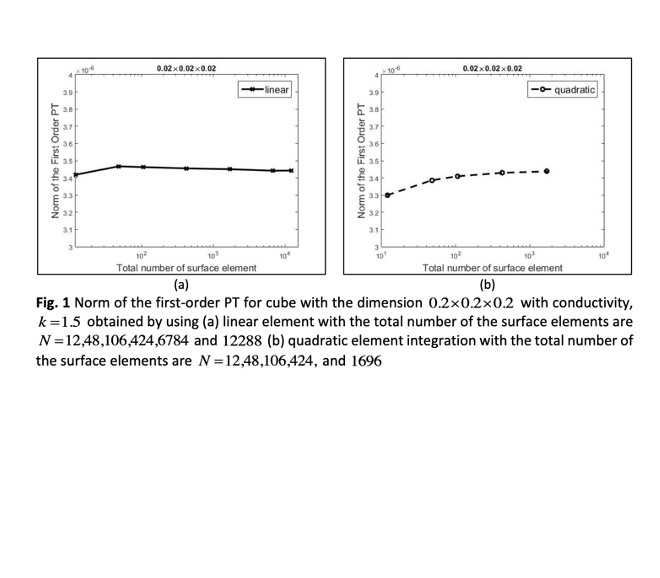
Polarization tensor (PT) is a classical terminology in fluid mechanics and theory of electricity that can describe geometry in a specific boundary domain with different conductivity contrasts. In this regard, the geometry may appear in a different size, and for easy characterizing, the usage of PT to identify particular objects is crucial. Hence, in this paper, the first order polarization tensor for different types of objects with a diverse range of sizes are presented. Here, we used three different geometries: sphere, ellipsoid, and cube, with fixed conductivity for each object. The software Matlab and Netgen Mesh Generator are the essential mathematical tools to aid the computation of the polarization tensor. From the analytical results obtained, the first order PT for sphere and ellipsoid depends on the size of both geometries. On the other hand, the numerical investigation is conducted for the first order PT for cube, since there is no analytical solution for the first order PT related to this geometry, to further verify the scaling property of the first order PT due to the scaling on the size of the original related object. Our results agree with the previous theoretical result that the first order polarization tensor of any geometry will be scaled at a fixed scaling factor according to the scaling on the size of the original geometry.