Semi- Analytical Study on Non-Isothermal Steady R-D Equation in a Spherical Catalyst and Biocatalyst
DOI:
https://doi.org/10.37934/cfdl.15.12.6076Keywords:
Lane–Emden equation, Spherical catalyst, Spherical biocatalyst, Ananthaswamy-Sivasankari method, Michaelis–Menten kinetics, Numerical simulation.Abstract
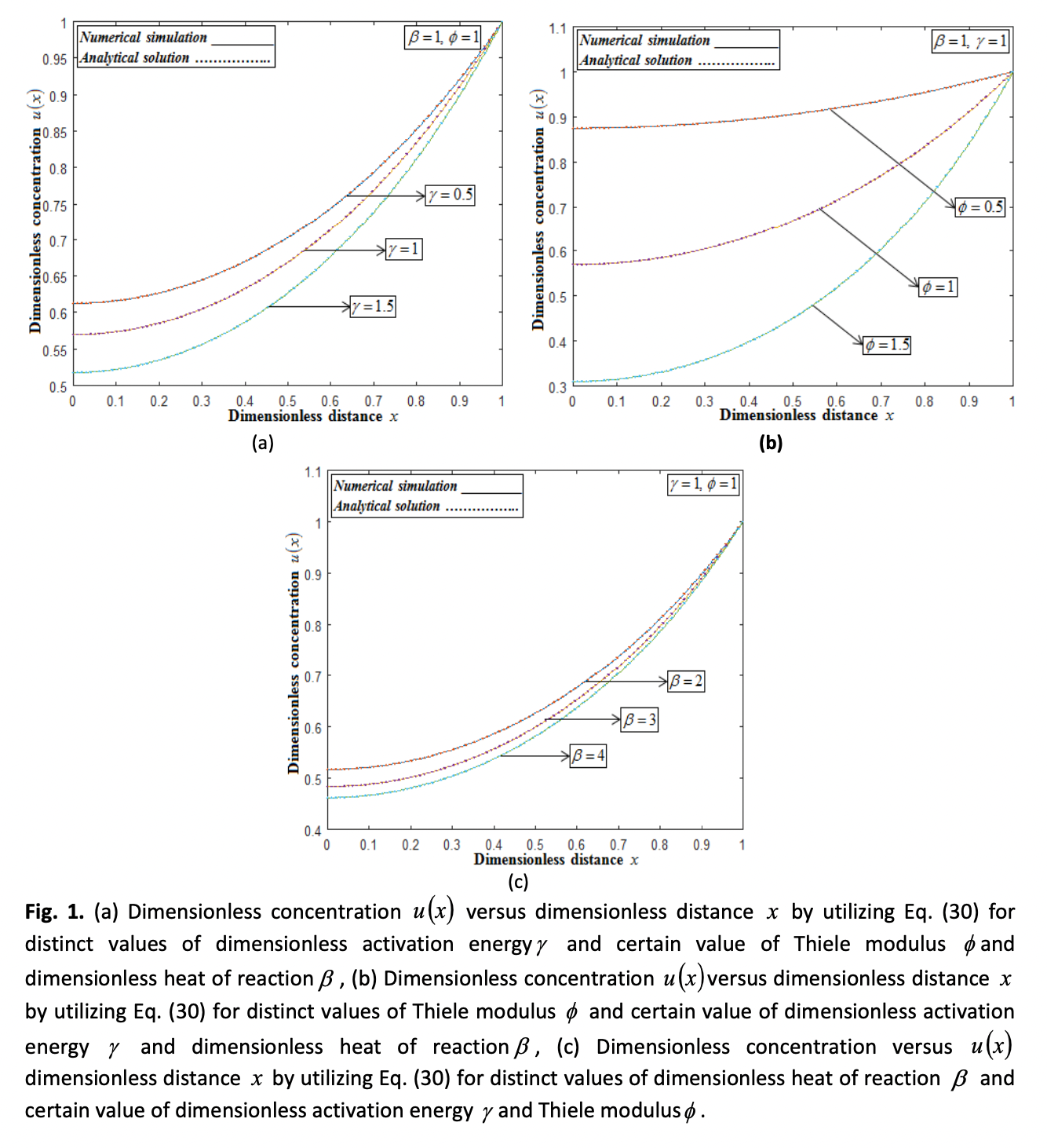
The Lane-Emden Boundary Value Problem as it appears in chemical applications, science, and biochemical applications are employed. Two specific models are solved by applying the Ananthaswamy-Sivasankari method (ASM). The model in first problem is a reaction–diffusion equation of a spherical catalyst and the model in second problem is the reaction–diffusion process of a spherical biocatalyst. Obtain a reliable semi-analytical expression of the effectiveness factors and the concentrations. A graph is constructed for the obtained semi-analytical solutions.The effects of several parameters like dimensionless activation energy, Thiele modulus and dimensionless heat of reaction are shown in graphical representation. Our semi-analytical solution is compared with numerical simulation by using MATLAB and finds good fit in all parameters. The new analytical method ASM is helpful to solve many non-linear problems mainly Reaction-Diffusion equation.
Downloads
References
Duggan, R. C., and A. M. Goodman. "Pointwise bounds for a nonlinear heat conduction model of the human head." Bulletin of mathematical biology 48 (1986): 229-236.https://doi.org/10.1007/BF02460025
Lin, S. H. "Oxygen diffusion in a spherical cell with nonlinear oxygen uptake kinetics." Journal of Theoretical Biology 60, no. 2 (1976): 449-457.https://doi.org/10.1016/0022-5193(76)90071-0
Rach, Randolph, Jun-Sheng Duan, and Abdul-Majid Wazwaz. "Solving coupled Lane–Emden boundary value problems in catalytic diffusion reactions by the Adomian decomposition method." Journal of Mathematical Chemistry 52 (2014): 255-267.https://doi.org/10.1007/s10910-013-0260-6
Rach, Randolph, Jun-Sheng Duan, and Abdul-Majid Wazwaz. "On the solution of non-isothermal reaction-diffusion model equations in a spherical catalyst by the modified Adomian method." Chemical Engineering Communications 202, no. 8 (2015): 1081-1088.https://doi.org/10.1080/00986445.2014.900054
Van Gorder, Robert A. "Exact first integrals for a Lane–Emden equation of the second kind modeling a thermal explosion in a rectangular slab." New Astronomy 16, no. 8 (2011): 492-497. https://doi.org/10.1016/j.newast.2011.04.006
Wazwaz, Abdul-Majid. "Solving the non-isothermal reaction-diffusion model equations in a spherical catalyst by the variational iteration method." Chemical Physics Letters 679 (2017): 132-136. https://doi.org/10.1016/j.cplett.2017.04.077
Duan, Jun-Sheng, Randolph Rach, and Abdul-Majid Wazwaz. "Steady-state concentrations of carbon dioxide absorbed into phenyl glycidyl ether solutions by the Adomian decomposition method." Journal of Mathematical Chemistry 53 (2015): 1054-1067. https://doi.org/10.1007/s10910-014-0469-z
Wazwaz, Abdul-Majid. "Solving systems of fourth-order Emden–Fowler type equations by the variational iteration method." Chemical Engineering Communications 203, no. 8 (2016): 1081-1092. https://doi.org/10.1080/00986445.2016.1141094
Wazwaz, Abdul-Majid. "The variational iteration method for solving new fourth-order Emden–Fowler type equations." Chemical Engineering Communications 202, no. 11 (2015): 1425-1437. https://doi.org/10.1080/00986445.2014.952814
Das, Nilima, Randhir Singh, Abdul-Majid Wazwaz, and Jitendra Kumar. "An algorithm based on the variational iteration technique for the Bratu-type and the Lane–Emden problems." Journal of Mathematical Chemistry 54 (2016): 527-551. https://doi.org/10.1007/s10910-015-0575-6
Kanth, ASV Ravi, and K. Aruna. "He’s variational iteration method for treating nonlinear singular boundary value problems." Computers & Mathematics with Applications 60, no. 3 (2010): 821-829. https://doi.org/10.1016/j.camwa.2010.05.029
Singh, Randhir, Jitendra Kumar, and Gnaneshwar Nelakanti. "Numerical solution of singular boundary value problems using Green’s function and improved decomposition method." Journal of Applied Mathematics and Computing 43 (2013): 409-425. https://doi.org/10.1007/s12190-013-0670-4
Singh, Randhir, Nilima Das, and Jitendra Kumar. "The optimal modified variational iteration method for the Lane-Emden equations with Neumann and Robin boundary conditions." The European Physical Journal Plus 132 (2017): 1-11. https://doi.org/10.1140/epjp/i2017-11521-x
Singh, Randhir, and Jitendra Kumar. "An efficient numerical technique for the solution of nonlinear singular boundary value problems." Computer Physics Communications 185, no. 4 (2014): 1282-1289. https://doi.org/10.1016/j.cpc.2014.01.002
Singh, Randhir, Jitendra Kumar, and Gnaneshwar Nelakanti. "Approximate series solution of nonlinear singular boundary value problems arising in physiology." The Scientific World Journal 2014 (2014). https://doi.org/10.1155/2014/945872
Singh, Randhir, and Jitendra Kumar. "The Adomian decomposition method with Green’s function for solving nonlinear singular boundary value problems." Journal of Applied Mathematics and Computing 44 (2014): 397-416. https://doi.org/10.1007/s12190-013-0699-4
Singh, Randhir, Sukhjit Singh, and Abdul-Majid Wazwaz. "A modified homotopy perturbation method for singular time dependent Emden–Fowler equations with boundary conditions." Journal of Mathematical Chemistry 54 (2016): 918-931. https://doi.org/10.1007/s10910-016-0594-y
Singh, Randhir, Abdul-Majid Wazwaz, and Jitendra Kumar. "An efficient semi-numerical technique for solving nonlinear singular boundary value problems arising in various physical models." International Journal of Computer Mathematics 93, no. 8 (2016): 1330-1346. https://doi.org/10.1080/00207160.2015.1045888
Singh, Randhir, and Abdul-Majid Wazwaz. "Numerical solution of the time dependent Emden–Fowler equations with boundary conditions using modified decomposition method." Appl. Math. Inf. Sci 10, no. 2 (2016): 403-408.doi:10.18576/amis/100203
Wazwaz, Abdul‐Majid, and Randolph Rach. "Comparison of the Adomian decomposition method and the variational iteration method for solving the Lane‐Emden equations of the first and second kinds." Kybernetes (2011). https://doi.org/10.1108/03684921111169404
Richardson, Owen Willans. The emission of electricity from hot bodies. Vol. 4. Longmans, Green and Company, 1921.
Sun, Yan-Ping, Shi-Bin Liu, and Scott Keith. "Approximate solution for the nonlinear model of diffusion and reaction in porous catalysts by the decomposition method." Chemical Engineering Journal 102, no. 1 (2004): 1-10. https://doi.org/10.1016/S1385-8947(03)00060-3
Wazwaz, Abdul‐Majid, Randolph Rach, and Jun‐Sheng Duan. "A study on the systems of the Volterra integral forms of the Lane–Emden equations by the Adomian decomposition method." Mathematical Methods in the Applied Sciences 37, no. 1 (2014): 10-19. https://doi.org/10.1002/mma.2776
Wazwaz, Abdul-Majid. "A new algorithm for solving differential equations of Lane–Emden type." Applied mathematics and computation 118, no. 2-3 (2001): 287-310. https://doi.org/10.1016/S0096-3003(99)00223-4
Wazwaz, Abdul-Majid. "A new method for solving singular initial value problems in the second-order ordinary differential equations." Applied Mathematics and computation 128, no. 1 (2002): 45-57. https://doi.org/10.1016/S0096-3003(01)00021-2
Wazwaz, Abdul-Majid. "Adomian decomposition method for a reliable treatment of the Bratu-type equations." Applied Mathematics and Computation 166, no. 3 (2005): 652-663. https://doi.org/10.1016/j.amc.2004.06.059
Wazwaz, Abdul-Majid, and Abdul-Majid Wazwaz. "Solitary waves theory." Partial Differential Equations and Solitary Waves Theory (2009): 479-502. https://doi.org/10.1007/978-3-642-00251-9_12
Wazwaz, Abdul-Majid, Randolph Rach, and Jun-Sheng Duan. "Adomian decomposition method for solving the Volterra integral form of the Lane–Emden equations with initial values and boundary conditions." Applied Mathematics and Computation 219, no. 10 (2013): 5004-5019. https://doi.org/10.1016/j.amc.2012.11.012
Flockerzi, Dietrich, and Kai Sundmacher. "On coupled Lane-Emden equations arising in dusty fluid models." In Journal of physics: conference series, vol. 268, no. 1, p. 012006. IOP Publishing, 2011. doi:10.1088/1742-6596 /268/1/012006
Muatjetjeja, Ben, and Chaudry Masood Khalique. "Noether, partial Noether operators and first integrals for the coupled Lane-Emden system." Mathematical and Computational Applications 15, no. 3 (2010): 325-333. https://doi.org/10.3390/mca15030325
Talwalkar, S., Mankar, S., Katariya, A., Aghalayam, P., Ivanova, M., Sundmacher, K. and Mahajani, S.“Selectivity engineering with reactive distillation for dimerization of C4 olefins: experimental and theoretical studies.” Industrial and Engineering Chemistry Research 46, (2007): 3024–3034. https://doi.org/10.1021/ie060860+
Zou, Henghui. "A priori estimates for a semilinear elliptic system without variational structure and their applications." Mathematische Annalen 323 (2002): 713-735. https://doi.org/10.1007/s002080200324
Connors, Kenneth Antonio. Chemical kinetics: the study of reaction rates in solution. Wiley-VCH Verlag GmbH, 1990.
Wazwaz, Abdul-Majid. "The variational iteration method for solving systems of equations of Emden–Fowler type." International Journal of Computer Mathematics 88, no. 16 (2011): 3406-3415. https://doi.org/10.1080/00207160.2011.587513
Wazwaz, Abdul-Majid. "The variational iteration method for solving the Volterra integro-differential forms of the Lane–Emden equations of the first and the second kind." Journal of Mathematical Chemistry 52, no. 2 (2014): 613-626. https://doi.org/10.1007/s10910-013-0281-1
Saadatmandi, Abbas, Nafiseh Nafar, and Seyed Pendar Toufighi. "Numerical study on the reaction cum diffusion process in a spherical biocatalyst." (2014): 47-61. https://doi.org/10.22052/IJMC.2014.5539
Randhir Singh. "Optimal homotopy analysis method for the non-isothermal reaction–diffusion model equations in a spherical catalyst." Journal of Mathematical Chemistry 56, no. 9 (2018): 2579-2590. https://doi.org/10.1007/s10910-018-0911-8
Ananthaswamy, V., Shanthakumari, R. and Subha, M.“Simple analytical expressions of the non–linear reaction diffusion process in an immobilized biocatalyst particle using the new homotopy perturbation method.” Review of Bioinformatics and Biometrics 3, (2014): 23–28.
He, Ji-Huan. "Variational iteration method for autonomous ordinary differential systems." Applied mathematics and computation 114, no. 2-3 (2000): 115-123. https://doi.org/10.1016/S0096-3003(99)00104-6
Liao, Shijun, Jian Su, and Allen T. Chwang. "Series solutions for a nonlinear model of combined convective and radiative cooling of a spherical body." International Journal of Heat and Mass Transfer 49, no. 15-16 (2006): 2437-2445. https://doi.org/10.1016/j.ijheatmasstransfer.2006.01.030
Weisz, P. B., and J. S. Hicks. "The behaviour of porous catalyst particles in view of internal mass and heat diffusion effects." Chemical Engineering Science 17, no. 4 (1962): 265-275. https://doi.org/10.1016/0009-2509(62)85005-2
Chitra, J., Ananthaswamy,V., Sivasankari,S. and Seenith Sivasundaram. “A new approximate analytical method (ASM) for solving non-linear boundary value problem in heat transfer through porous fin.” Mathematics in Engineering, Science and Aerospace (MESA) (ISSN: 2041-3065) 14, no. 1 (2023): 53-69.
Sivasankari, S., Ananthaswamy,V. and Seenith Sivasundaram. “A new approximate analytical method for solving some non-linear initial value problems in physical sciences.” Mathematics in Engineering, Science and Aerospace (MESA) (ISSN: 2041-3065) 14, no. 1 (2023): 145-162.
Ala’yed, O., Saadeh, R., & Qazza, A. (2023). Numerical solution for the system of Lane-Emden type equations using cubic B-spline method arising in engineering. AIMS Mathematics, 8(6), 14747-14766. https://doi:10.3934/math.203754
Omaba, M. E. (2022). New analytical method of solution to a nonlinear singular fractional Lane–Emden type equation. AIMS Mathematics, 7(10), 19539-19552. https://doi:10.3934/math.20221072
Rach, R., Duan, J. S., & Wazwaz, A. M. (2015). On the solution of non-isothermal reaction-diffusion model equations in a spherical catalyst by the modified Adomian method. Chemical Engineering Communications, 202(8), 1081-1088. https://doi.org/10.1080/00986445.2014.900054
Fogler, H. S. (1999). Elements of chemical reaction engineering, 3rd.
Danish, M., Kumar, S., & Kumar, S. (2011). OHAM solution of a singular BVP of reaction cum diffusion in a biocatalyst. IAENG International Journal of Applied Mathematics, 41(3), 223-227.
Fogler, H.S. (1997). Elements of Chemical Reaction Engineerring: 2nd Edition. New Jersey: Prentice-Hall Inc.
Skrzypacz, P., Andreev, V. V., & Golman, B. (2020). Dead-core and non-dead-core solutions to diffusion-reaction problems for catalyst pellets with external mass transfer. Chemical Engineering Journal, 385, 123927. https://doi.org/10.1016/j.cej.2019.123927
Golman, B., Andreev, V. V., & Skrzypacz, P. (2020). Dead-core solutions for slightly non-isothermal diffusion-reaction problems with power-law kinetics. Applied Mathematical Modelling, 83, 576-589. https://doi.org/10.1016/j.apm.2020.03.016
Crasta, A., Pathan, K. A., & Khan, S. A. (2023). Analytical and Numerical Simulation of Surface Pressure of an Oscillating Wedge at Hypersonic Mach Numbers and Application of Taguchi's Method. Journal of Advanced Research in Applied Sciences and Engineering Technology, 30(1), 15-30. https://doi.org/10.37934/araset.30.1.1530
Jamal Ghouizi, Mohamed Nabou, Mohammed Elmir, Mohamed Douha, and Mehdi Berramdane. “Numerical Simulation of Natural Convetion in A Cavity Filled with A Nanofluid Who’s Wall Containing the Heat source is Inclined.” Journal of Advanced Research in Fluid Mechanics and Termal Sciences 76, no.1, (2020), 1-16. https://doi.org/10.37934/arfmts.76.1.116