A Study of Geometrical Effects on Permeability Estimation in Three-dimensional Fractures Using the Lattice Boltzmann Method
DOI:
https://doi.org/10.37934/cfdl.15.12.118Keywords:
fractures, The Lattice Boltzmann Method, mean aperture, surface roughness, permeabilityAbstract
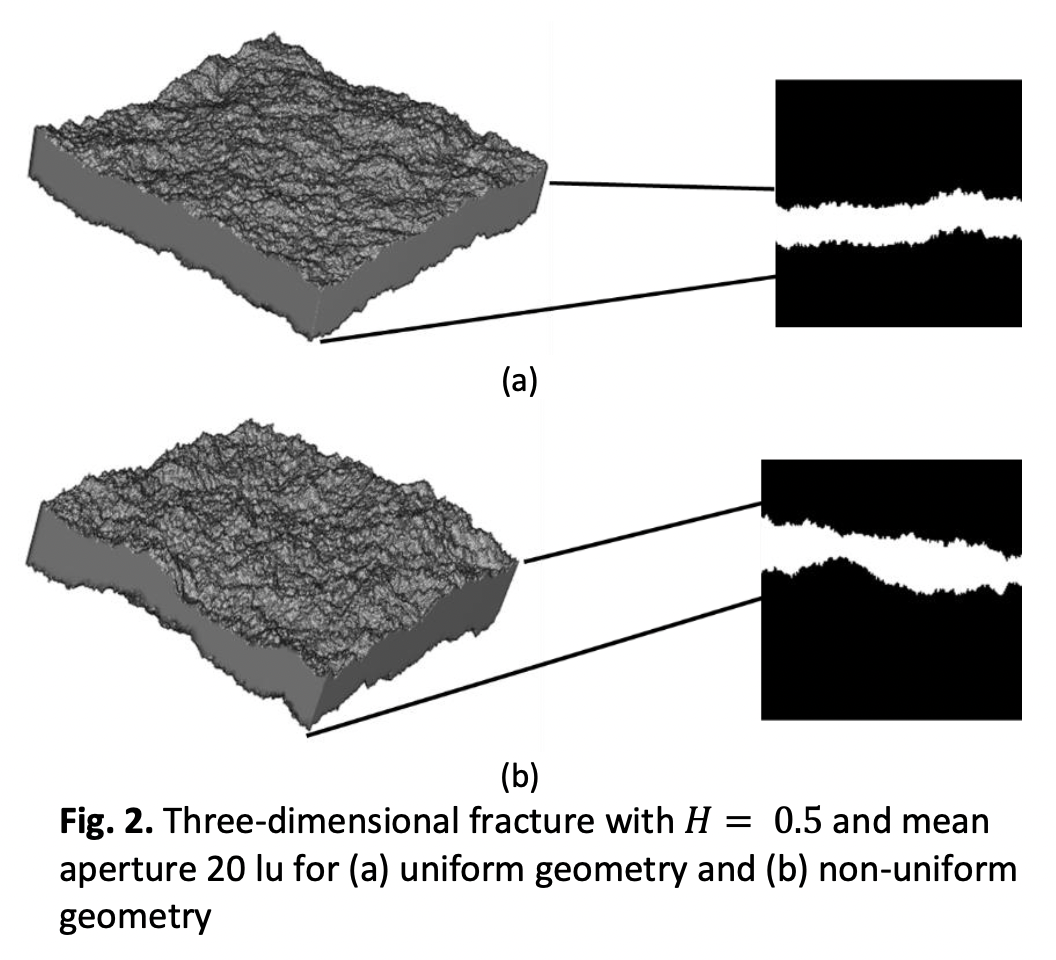
This study investigates the effect of geometry on permeability estimation in three-dimensional fractures using the Lattice Boltzmann Method. Fractures have irregular and complex shapes, which can significantly impact their permeability. Anisotropy of permeability is important as it indicates the influence of changes in fracture orientation on the flow and transport properties of fluids. To examine the relationship between permeability and fracture geometry, we generated three-dimensional fracture geometries using fractal Brownian motion with a Hurst exponent to describe the roughness on the fracture surface. The fractures in this study have varying mean aperture, ranging from narrow to wide, with surface roughness that can be either uniform or non-uniform. The Lattice Boltzmann Method was performed to calculate permeability and investigate the relationship between permeability and geometric parameters of fractures, such as mean aperture and surface roughness. Our results were in good agreement with previous studies on two-dimensional fractures. We found a clear relationship between permeability and mean aperture. Both in uniform and non-uniform geometry have the same trend as the mean aperture increased, permeability generally increased, while rougher surface roughness permeability generally decreased but in non-uniform geometry the data on the graph appears more random and irregular. We extended our investigation to real fractures by digital rock portal data. The analysis revealed that the geometry of the real fractures closely resembled non-uniform geometry, and the permeability exhibited anisotropic behaviour. In addition, the anisotropy of permeability and computation time were also investigated; and it was found that both can be influenced by the three-dimensional fracture geometry.
Downloads
References
Gunde, Akshay. “Spontaneous imbibition and solvent diffusion in fractured porous media by LBM.” (2011). https://doi.org/10.7939/R3572K
Guo, Boyun, Kai Sun, and Ali Ghalambor. Well productivity handbook. Elsevier, 2014.
https://doi.org/10.1016/b978-1-933762-32-6.50010-7.
Herdiansyah, Herdis, Habibullah Adi Negoro, Nurul Rusdayanti, and Siti Shara. “Palm oil plantation and cultivation: Prosperity and productivity of smallholders.” Open Agriculture 5, no. 1 (2020): 617-630. https://doi.org/10.1515/opag-2020-0063
Wynn, Tim. “Introduction to Naturally Fractured Reservoirs Part 1 – Fracture Origins, Characteristics and Parameters.” First Break 40, no. 7 (2022): 31-40. https://doi.org/10.3997/1365-2397.fb2022054
Askari, Amir Abbas, Golamreza Bashiri, and Mohammad Reza Kamali. “Model ranking and optimization of fractured reservoir using streamline simulation, case study a gas condensate reservoir.” In SPE Saudi Arabia Section Technical Symposium. OnePetro, 2009. https://doi.org/10.2118/126074-MS
Sahimi, Muhammad. Flow and transport in porous media and fractured rock: from classical methods to modern approaches. John Wiley & Sons, 2011. https://doi.org/10.1002/9783527636693
Jing, Lanru, and Ove Stephansson. “The basics of fracture system characterization–Field mapping and stochastic simulations.” In Developments in geotechnical engineering, vol. 85, pp. 147-177. Elsevier, 2007. https://doi.org/10.1016/S0165-1250(07)85005-X
Chen, Tao, and Jean Borgomano. “The Impact of Fracture Geometries on Heterogeneity and Accuracy of Upscaled Equivalent Fracture Models.” Lithosphere 2022, no. 1 (2022). https://doi.org/10.2113/2022/5070481
Wang, Kang, Suping Peng, Yongxu Lu, and Xiaoqin Cui. “Wavefield simulation of fractured porous media and propagation characteristics analysis.” Geophysical Prospecting 70, no. 5 (2022): 886-903. https://doi.org/10.1111/1365-2478.13198
Zhao, Yan-long, Zhi-ming Wang, Jian-ping Ye, Han-sen Sun, and Jiao-yang Gu. “Lattice Boltzmann simulation of gas flow and permeability prediction in coal fracture networks.” Journal of Natural Gas Science and Engineering 53 (2018): 153-162. https://doi.org/10.1016/j.jngse.2018.03.001
Zhang, Yao, and Junrui Chai. “Effect of surface morphology on fluid flow in rough fractures: a review.” Journal of Natural Gas Science and Engineering 79 (2020): 103343. https://doi.org/10.1016/j.jngse.2020.103343
National Research Council. Rock fractures and fluid flow: contemporary understanding and applications. National Academies Press, 1996. https://doi.org/10.17226/2309
Dou, Zhi, and Zhi-fang Zhou. “Lattice Boltzmann simulation of solute transport in a single rough fracture.” Water Science and Engineering 7, no. 3 (2014): 277-287. https://doi.org/10.3882/j.issn.1674-2370.2014.03.004
Dharmawan, I. A., R. Z. Ulhag, C. Endyana, and Muhammad Aufaristama. “Numerical simulation of non-Newtonian fluid flows through fracture network." In IOP conference series: earth and environmental science, vol. 29, no. 1, p. 012030. IOP Publishing, 2016. https://doi.org/10.1088/1755-1315/29/1/012030
Wang, Min, Yi-Feng Chen, Guo-Wei Ma, Jia-Qing Zhou, and Chuang-Bing Zhou. "Influence of surface roughness on nonlinear flow behaviours in 3D self-affine rough fractures: Lattice Boltzmann simulations.” Advances in water resources 96 (2016): 373-388. https://doi.org/10.1016/j.advwatres.2016.08.006
Zhang, Min, Maša Prodanović, Maryam Mirabolghasemi, and Jianlin Zhao. “3D microscale flow simulation of shear-thinning fluids in a rough fracture.” Transport in Porous Media 128 (2019): 243-269. https://doi.org/10.1007/s11242-019-01243-9
Tian, Xu, Yinger Deng, Dang Jing, Xin Peng, and Mubai Duan. “Research on the influence of geometry on nonlinear flow in constructed rough fractures by lattice Boltzmann simulation.” Arabian Journal of Geosciences 13 (2020): 1-18. https://doi.org/10.1007/s12517-019-5051-3
Irayani, Z., U. Fauzi, S. Viridi, and F. D. E. Latief. "Calculation of anisotropy permeability from 3D tomographic images using renormalization group approaches and lattice Boltzmann method." Journal of Petroleum Exploration and Production Technology 9 (2019): 889-897. https://doi.org/10.1007/s13202-018-0558-9
Niya, SM Rezaei, and A. P. S. Selvadurai. "Correlation of joint roughness coefficient and permeability of a fracture." International Journal of Rock Mechanics and Mining Sciences 113 (2019): 150-162. https://doi.org/10.1016/j.ijrmms.2018.12.008
Yin, Peijie, Can Zhao, Jianjun Ma, and Linchong Huang. “A unified equation to predict the permeability of rough fractures via lattice Boltzmann simulation.” Water 11, no. 5 (2019): 1081. https://doi.org/10.3390/w11051081
Chaabane, Raoudha, Nor Azwadi Che Sidik, and Abdelmajid Jemni. "Convective Boundary Conditions Effect on Cylindrical Media with Transient Heat Transfer." Journal of Advanced Research in Fluid Mechanics and Thermal Sciences 82, no. 2 (2021): 146-156. https://doi.org/10.37934/arfmts.82.2.146156
Zhao, Huawei, Zhengfu Ning, Qinjun Kang, Li Chen, and Tianyi Zhao. “Relative permeability of two immiscible fluids flowing through porous media determined by lattice Boltzmann method.” International Communications in Heat and Mass Transfer 85 (2017): 53-61. https://doi.org/10.1016/j.icheatmasstransfer.2017.04.020
Sidik, Nor Azwadi Che, Raoudha Chaabane, and Hong Wei Xian. "Heat Transfer Study in Cylindrical Cavity with Heat Absorption or Generation." Journal of Advanced Research in Applied Sciences and Engineering Technology 27, no. 2 (2022): 16-27. https://doi.org/10.37934/araset.27.2.1627
Xiao, Feng, and Xiaolong Yin. “Geometry models of porous media based on Voronoi tessellations and their porosity–permeability relations.” Computers & Mathematics with Applications 72, no. 2 (2016): 328-348.
https://doi.org/10.1016/j.camwa.2015.09.009
Zhao, Yanlong, Zhiming Wang, Quanshu Zeng, Jiangtao Li, and Xiao Guo. “Lattice Boltzmann simulation for steady displacement interface in cementing horizontal wells with eccentric annuli.” Journal of Petroleum Science and Engineering 145 (2016): 213-221. https://doi.org/10.1016/j.petrol.2016.04.005
Jin, Yi, Jiabin Dong, Xiangyu Zhang, Xiang Li, and Ying Wu. “Scale and size effects on fluid flow through self-affine rough fractures.” International Journal of Heat and Mass Transfer 105 (2017): 443-451. https://doi.org/10.1016/j.ijheatmasstransfer.2016.10.010
Ávila, Joseph, Javier Pagalo, and Mayken Espinoza-Andaluz. “Evaluation of geometric tortuosity for 3D digitally generated porous media considering the pore size distribution and the A-star algorithm.” Scientific Reports 12, no. 1 (2022): 19463. https://doi.org/10.1038/s41598-022-23643-6
Muntashir, A. W. and Irwan Ary D.”Smartfract” SmartFract, 2015, http:/grid.unpad.ac.id/~smartfract2/.
Madadi, Mahyar, Clinton D. VanSiclen, and Muhammad Sahimi. “Fluid flow and conduction in two‐dimensional fractures with rough, self‐affine surfaces: A comparative study.” Journal of Geophysical Research: Solid Earth 108, no. B8 (2003). https://doi.org/10.1029/2002JB002332
Odling, Noelle E. "Natural fracture profiles, fractal dimension and joint roughness coefficients." Rock mechanics and rock engineering 27 (1994): 135-153. https://doi.org/10.1007/BF01020307
Schmittbuhl, J., A. Steyer, L. Jouniaux, and Renaud Toussaint. "Fracture morphology and viscous transport." International Journal of Rock Mechanics and Mining Sciences 45, no. 3 (2008): 422-430. https://doi.org/10.1016/j.ijrmms.2007.07.007
Auradou, Harold. "Influence of wall roughness on the geometrical, mechanical and transport properties of single fractures." Journal of Physics D: Applied Physics 42, no. 21 (2009): 214015. https://doi.org/10.1088/0022-3727/42/21/214015
Karpyn, Zuleima, Christopher Landry, and Masa Prodanovic. ‘Induced Rough Fracture in Berea Sandstone Core’. Digital Rocks Portal, 2016. https://doi.org/10.17612/P7J012
Latt, Jonas, Orestis Malaspinas, Dimitrios Kontaxakis, Andrea Parmigiani, Daniel Lagrava, Federico Brogi, Mohamed Ben Belgacem et al., “Palabos: parallel lattice Boltzmann solver.” Computers & Mathematics with Applications 81 (2021): 334-350. https://doi.org/10.1016/j.camwa.2020.03.022
Azmi, Mohd Irwan Mohd, Nor Azwadi Che Sidik, Yutaka Asako, Wan Mohd Arif Aziz Japar, Nura Muaz Muhammad, and Nadlene Razali. "Numerical Studies on PCM Phase Change Performance in Bricks for Energy-Efficient Building Application–A Review." Journal of Advanced Research in Numerical Heat Transfer 1, no. 1 (2020): 13-21.
Huang, Haibo, Michael Sukop, and Xiyun Lu. “Multiphase lattice Boltzmann methods: Theory and application.” (2015). https://doi.org/10.1002/9781118971451
Sukop, M. C. "DT Thorne, Jr. Lattice Boltzmann Modeling Lattice Boltzmann Modeling." (2006). https://doi.org/10.1007/978-3-540-27982-2
Guiltinan, Eric J., Javier E. Santos, M. Bayani Cardenas, D. Nicolas Espinoza, and Qinjun Kang. "Two‐Phase Fluid Flow Properties of Rough Fractures With Heterogeneous Wettability: Analysis With Lattice Boltzmann Simulations." Water Resources Research 57, no. 1 (2021): e2020WR027943. https://doi.org/10.1029/2020WR027943